Simple Percptrons(简单感知机)

supervised learning(learning with a teacher)监督学习

5.1 Feed-Forward Networks

Perceptrons: layered feed-forward networks(分层前馈网络).

one-layer and two-layer(hidden units) perceptrons. $N$-layer network has $N$ layers of connections and $N — 1$ hidden layers.

asymmetric connection matrices $w_{ij}$(triangular matrix, 三角矩阵): no energy function exists. 只有对称阵存在能量函数

$$ H = -\frac{1}{2}\sum_{ij}w_{ij}S_{i}S_{j} $$

Simple perceptron(no hidden units). Input: $\xi_{k}$; Output: $O_{i}$.

$$ O_{i} = g(h_{i}) = g\left(\sum_{k}w_{ik}\xi_{k}\right),\quad g(h): \text{activation function} $$

Output is an explicit(显式) function of the input.

阈值可以被处理为一个等效的输入节点 $\xi_{0} = - 1$, 且权重 $w_{i0} = \theta_{i}$.

$$ O_{i} = g\left(\sum_{k=0}^{N}w_{ik}\xi_{k}\right) = g\left(\sum_{k=1}^{N}w_{ik}\xi_{k}-\theta_{i}\right) $$

目标: 若 input $\xi_{k}^{\mu}$ 所得的 output 为 $O_{i}^{\mu}$, 要求 the general association task: $O_{i}^{\mu} = \zeta_{i}^{\mu}$(target pattern).

其中 $k$ 为 input 节点标记, $i$ 为 output 节点标记, $\mu=1,\cdots,p$ 为 pattern/pairs 标记.

boolean($\pm 1$) / continuous-valued.

• auto-association task(自关联任务): 输入 pattern $\xi_{k}^{\mu}$, 输出 pattern 也是 $\xi_{k}^{\mu}$.

• hetero-association task(异关联任务): 输入 pattern $\xi_{k}^{\mu}$, 输出 pattern 为 $\zeta_{i}^{\mu}$. 通常输入与输出的 units 数不同.

classification problems: inputs 会被分到不同 categories.

find the weights $w_{ik}$ in a finite number of steps.

5.2 Threshould Units(阈值单元)

设 $g(h) = \text{sgn}(h)$, target $\zeta_{i}^{\mu} = \pm 1$.

由于 output unit 彼此独立, 不失一般性地, 省略 output 标记 $i$: $\vec{w} = (w_{1},w_{2},\cdots,w_{N})$.

input pattern $\vec{\xi}^{\mu}\in\mathbb{R}^{N}$.

那么求和形式可写作矢量内积形式:

$$ \sum_{k}w_{k}\xi_{k}^{\mu} = \vec{w}\cdot\vec{\xi}_{\mu},\quad \text{sgn}(\vec{w}\cdot\vec{\xi}_{\mu}) = \zeta^{\mu} $$

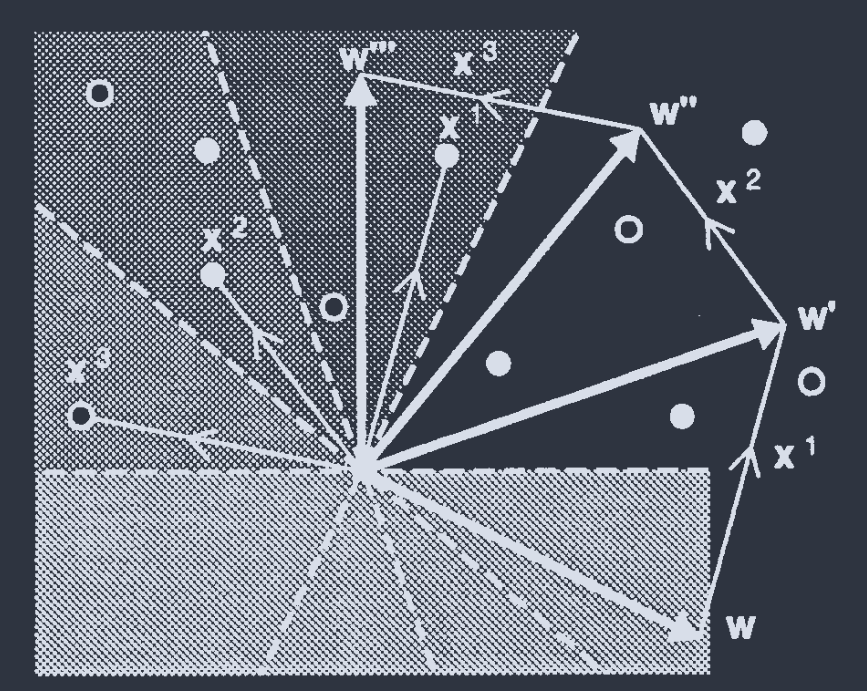
通过选择 $\vec{w}$, 使得 $\vec{\xi}_{\mu}$ 在其投影(projection) 和 $\zeta^{\mu}$ 同号. 存在临界 $\vec{w}\cdot\vec{\xi}_{\mu} = 0$, 即两者正交.

(a) 通过合适的 $\vec{w}$, 使得实心圆($\zeta^{\mu}=+1$)和空心圆($\zeta^{\mu}=-1$)被超平面分开.

(b) 通过合适的 $\vec{w}$, 使得所有圆都在超平面(hyperplane)法向量 $\vec{w}$ 所指的一侧.

定义辅助矢量 $\vec{x}^{\mu}\equiv \zeta^{\mu}\vec{\xi}$, 从而条件写作

$$ \vec{w}\cdot\vec{x}^{\mu} > 0 $$

也可将求和项具体展开, 补上原先忽略的指标 $i$:

$$ \sum_{k}w_{ik}\zeta^{\mu}\xi_{k}^{\mu} = \zeta^{\mu}\left(\sum_{k}w_{ik}\xi_{k}^{\mu}\right) = \zeta^{\mu}h_{i}^{\mu} > 0 $$

Linear Separability(线性可分性)

超平面是否存在, 决定分类问题是否可通过 perceptron 解, 或线性可分(linearly separable).

输出

$$ O_{i} = \text{sgn}\left(\sum_{k>0}w_{ik}\xi_{k}-w_{i0}\right) \Leftarrow O = \text{sgn}\left(\vec{w}\cdot\vec{\xi}-w_{0}\right) $$

那么 $N-1$ 维超平面是由

$$ \vec{w}\cdot\vec{\xi} = w_{0} \Leftrightarrow \hat{n}\cdot\vec{\xi} = \frac{w_{0}}{||\vec{w}||} $$

决定的. 其中定义法向单位向量 $\hat{n} = \frac{\vec{w}}{||\vec{w}||}$, 可见阈值 $w_{0}$ 的作用是使得超平面沿着 $\vec{w}$ 方向从原点偏移 $\frac{w_{0}}{||\vec{w}||}$.

AND function/Truth table

$\xi$: on = 1; off = 0.

$\zeta$: true = 1; false = -1.

$\xi_{1}$	$\xi_{2}$	$\zeta$
0	0	-1
0	1	-1
1	0	-1
1	1	+1

“且” 问题是线性可分的. (b) 给出了一个可能的网络示例.

定义阈值所用的等效节点 $\xi_{0} = -1$, 则 “且” 问题化为 3D 图示

由于所有 input($\vec{\xi}_{\mu}$) 都偏移了一个矢量 $(0,0,\cdots,w_{0})$, 那么这个点成为事实上的新原点. 于是回归到无阈值情况, 超平面经过新原点.

非线性可分问题: XOR function(异或问题, 同为假, 异为真)

$\xi_{1}$	$\xi_{2}$	$\zeta$
0	0	-1
0	1	+1
1	0	+1
1	1	-1

(a) XOR (b) 三点共线的概率为 0.

对 general position 的解读:

• 除开这类特殊情况, 点集处于 general position.
• $N$ 维空间中, 取任意 $d<N$ 维超平面, 其所含点数不超过 $d+1$. 则点集处于 general position.
• 无阈值问题时, 等价为任意 $d\leq N$ 个点彼此线性独立(不共面).

A Simple Learning Algorithm

$$ \begin{aligned} w_{ik}^{\prime} = w_{ik} + \Delta w_{ik},\quad \Delta w_{ik} = \begin{cases} 2\eta \zeta_{i}^{\mu}\xi_{k}^{\mu} & \text{if }\zeta_{i}^{\mu}\neq O_{i}^{\mu};\\ 0 & \text{otherwise} \end{cases} \end{aligned} $$

其中

$$ \Delta w_{ik} = \eta(1-\zeta_{i}^{\mu}O_{i}^{\mu})\zeta_{i}^{\mu}\xi_{k}^{\mu} = \eta(\zeta_{i}^{\mu} - O_{i}^{\mu})\xi_{k}^{\mu}; \quad \text{since }\zeta_{i}^{\mu}, O_{i}^{\mu} = \pm 1 $$

两种表述是等价的, 只是后者去掉了条件判断.

$\eta>0$: learning rate(学习率).

Will it work?

• 若已经正确分类($O_{i}^{\mu} = \zeta_{i}^{\mu}$), 则权重无需更新. 此时 $\zeta_{i}^{\mu}O_{i}^{\mu} = +1$;
• 若误分类($O_{i}^{\mu} = -\zeta_{i}^{\mu}$), 既然目标也可写作形式 $\vec{w}\cdot\vec{x}^{\mu}>0$, 不难注意到学习算法也可以写作 $\Delta w_{ik} = 2\eta x_{ik}^{\mu}$, 这使得 $$ w^{\prime}_{i}\cdot\vec{x}^{\mu} = \sum_{k}(w_{ik} + \Delta w_{ik})x_{ik}^{\mu} = \sum_{k}(w_{ik} + 2\eta x_{ik}^{\mu})x_{ik}^{\mu} = \vec{w}_{i}\cdot \vec{x}_{i}^{\mu} + \Delta,\quad \Delta > 0 $$

$\Delta$ 项使得 $w_{i}^{\prime}\cdot\vec{x}^{\mu}_{i}$ 必定递增, 从而达成 $w_{i}^{\prime}\cdot\vec{x}^{\mu}_{i}>0$ 的目标.

$$ \begin{aligned} \zeta_{i}^{\mu}h_{i}^{\mu} &\equiv \zeta_{i}^{\mu}\sum_{k}w_{ik}\xi_{k}^{\mu} \\ &= \sum_{k}w_{ik} (\zeta_{i}^{\mu}\xi_{k}^{\mu}) = \vec{w}\cdot\vec{x}^{\mu}> N\kappa \end{aligned} $$

第二行是另一种目标的等价表达.

其中 $\kappa$ 被称作 margin size, 这是为了防止某些 $\vec{\xi}^{\mu}$ 非常接近超平面, 导致噪声或误差使得误分类. 添加 $N$ 使得任意 input unit 数均可工作.

将 $N\kappa$ 视为阈值, 那么学习算法改进为

$$ \Delta w_{ik} = \eta\Theta(N\kappa-\zeta_{i}^{\mu}h_{i}^{\mu})\zeta_{i}^{\mu}\xi_{k}^{\mu},\quad\Theta(x) = \begin{cases} 1 & \text{if } x > 0;\\ 0 & \text{otherwise} \end{cases} $$

若存在输出节点 $i$ 有 $N\kappa > \zeta_{i}^{\mu}h_{i}^{\mu}$, 说明未达成目标, 需要通过 $\vec{x}^{\mu}_{i}$ 继续增大 $\Delta w_{ik}$, 从而产生演化 $w\rightarrow w^{\prime}\rightarrow w^{\prime\prime}\rightarrow \cdots$

当 $\kappa=0$, 退化为原算法形式.

写作矢量形式:

$$ \Delta \vec{w} = \eta\Theta(N\kappa-\vec{w}\cdot\vec{x}^{\mu})\vec{x}^{\mu} $$

$\kappa = 0, \eta = 1$. 每次都会找到与超平面异侧的点, 那么优化 $\vec{w}$ 时令其加上对应点矢, 直至所有点均在超平面 $\vec{w}$ 所指一侧为止.

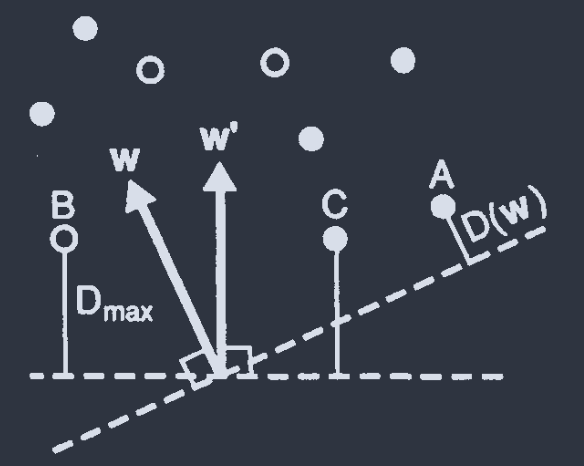
$\vec{x}^{\mu}$ 到超平面的距离决定了分类问题的难易程度. 定义

$$ D(\vec{w}) = \frac{1}{||\vec{w}||}\underset{\mu}{\text{min }}\vec{w}\cdot\vec{x}^{\mu} $$

是各点到超平面的最小距离.

Optimal perceptron 致力于寻找使得 $D$ 最大化的 $\vec{w}$:

$$ D_{\text{max}} \equiv \underset{\vec{w}}{\text{max }}D(\vec{w}) $$

一般性权重 $\vec{w}$ 和 optimal $\vec{w}^{\prime}$.

$D_{\text{max}}$ 越大, 问题越简单. $D_{\text{max}}<0$, 问题不可解.

5.3 Proof of Convergence of the Perceptron Learning Rule

Perceptron learning rule reaches a solution in a finite number of steps.

设 $\vec{w}^{*}$ 为一已知解($D(\vec{w}^{*})>0$).

设初始权重 $\vec{w}_{0}=0$. 令 $M^{\mu}$ 为模式 $\mu$ 更新次数. 更新后权重为

$$ \vec{w} = \vec{w}_{0} + \sum\Delta\vec{w} = \eta\sum_{\mu}M^{\mu}\vec{x}^{\mu},\quad M = \sum_{\mu}M^{\mu} $$

计算更新后权重 $\vec{w}$ 和已知权重解 $\vec{w}^{*}$ 内积:

$$ \begin{aligned} \vec{w}\cdot\vec{w}^{*} &= \eta\sum_{\mu}M^{\mu}\vec{x}^{\mu}\cdot\vec{w}^{*}\geq \eta M\underset{\mu}{\text{min }}\vec{x}^{\mu}\cdot\vec{w}^{*} = \eta M D(\vec{w}^{*})||\vec{w}^{*}||\sim M\\ &\Rightarrow \vec{w^{*}}\cdot\frac{\vec{w}}{||\vec{w}||}\sim M \end{aligned} $$

这表明, 如果 $M$ 不是有限值, $\vec{w}^{*}$ 在 $\vec{w}$ 方向上的投影将会发散, 这和 $\vec{w^{*}}\cdot\frac{\vec{w}}{||\vec{w}||}\leq ||\vec{w}^{*}||$ 显然是矛盾的.

若模式 $\alpha$ 在误分类而需更新, 更新后模长平方变化为

$$ \begin{aligned} \Delta(||\vec{w}||^{2}) &= (\vec{w}+\eta\vec{x}^{\alpha})^{2} - (\vec{w})^{2} = \eta^{2}(\vec{x}^{\alpha})^{2} + 2\eta\vec{w}\cdot\vec{x}^{\alpha}\\ &\leq \eta^{2} N + 2\eta N\kappa = N\eta(\eta + 2\kappa) \end{aligned} $$

• 学习算法目标的判别式也可写作 $\vec{w}\cdot\vec{x}^{\mu}>N\kappa$, 既然 $\mu = \alpha$ 时误分类, 则 $\vec{w}\cdot\vec{x}^{\alpha}\leq N\kappa$;
• $x_{k}^{\alpha} = \pm 1$, 所以 $(\vec{x}^{\alpha})^{2} = \sum_{k}^{N}(x_{k}^{\alpha})^{2} = N$.

所以 $||\vec{w}||^{2}$ 存在上界

$$ ||\vec{w}||^{2} \leq M [\Delta (||\vec{w}||^{2})] \leq M N\eta(\eta + 2\kappa)\\ \Rightarrow ||\vec{w}|| \sim \sqrt{M} $$

计算 $\vec{w}$ 与 $\vec{w}^{*}$ 夹角余弦平方:

$$ \phi = \frac{(\vec{w}\cdot\vec{w}^{*})^{2}}{||\vec{w}||^{2}||\vec{w}^{*}||^{2}}\leq 1 $$

前文讨论可得

$$ \begin{aligned} (\vec{w}\cdot\vec{w}^{*})^{2} &\geq \eta^{2} M^{2}D(\vec{w}^{*})^{2}||\vec{w}^{*}||^{2}\\ \frac{1}{||\vec{w}||^{2}} &\geq \frac{1}{MN\eta(\eta+2\kappa)} \end{aligned} $$

相乘可得

$$ 1 \geq \phi \geq M\frac{D(\vec{w}^{*})^{2}\eta}{N(\eta+2\kappa)} $$

所以 $M$ 存在上界

$$ M\leq N\frac{1 + 2\kappa/\eta}{D_{\text{max}}^{2}} $$

不显含模式数 $p$, 但通常会因为 $p\uparrow$ 而 $D_{\text{max}}\downarrow$, 从而使 $M\uparrow$.

5.4 Linear Units

由 $g(h)=\text{sgn}(h)$ 拓展到 连续且可导函数 $g(h)$. Linear units: $g(h)=h$.

目标写作

$$ \zeta_{i}^{\mu} = O_{i}^{\mu} = \sum_{k}w_{ik}\xi_{k}^{\mu} $$

$O_{i}^{\mu}$ 为连续值, 而 $\zeta_{i}^{\mu}=\pm 1$ 仍然是被允许的.

Explicit Solution(显式解)

auto-association: $\zeta_{i}^{\mu} = \xi_{i}^{\mu}$. 推广至 hetero-association:

$$ \begin{aligned} w_{ik} &= \frac{1}{N}\sum_{\mu\nu}\zeta_{i}^{\mu}(\mathbf{Q}^{-1})_{\mu\nu}\xi_{k}^{\nu}\\ \mathbf{Q}_{\mu\nu} &= \frac{1}{N}\sum_{k}\xi_{k}^{\mu}\xi_{k}^{\nu} \end{aligned} $$

Proof:

$$ \begin{aligned} O_{i}^{\lambda} \equiv \sum_{k}w_{ik}\xi_{k}^{\lambda} &= \frac{1}{N}\sum_{k}\sum_{\mu\nu}\zeta_{i}^{\mu}(\mathbf{Q}^{-1})_{\mu\nu}\xi_{k}^{\nu}\xi_{k}^{\lambda}\\ &= \sum_{\mu\nu}\zeta_{i}^{\mu}(\mathbf{Q}^{-1})_{\mu\nu}\mathbf{Q}_{\nu\lambda}\\ &= \sum_{\mu}\zeta_{i}^{\mu}\delta_{\mu\lambda} = \zeta_{i}^{\lambda} \end{aligned} $$

$\mathbf{Q}$ 的逆存在条件为满秩/${\xi_{k}^{\mu}}$ 线性无关(linearly independent). 由于 input units 数为 $N$, 因此能存储 $p\leq N$ 个线性无关的模式.

即使 $p<N$, 也不能保证其线性无关. 若存在关系 $\sum_{\mu=1}^{p}a_{k}\xi_{k}^{\mu} = 0$, 则 ${\xi_{k}^{p}}$ 只能张成模式子空间(pattern subspace). 可以找到 $\xi_{k}^{*}$ 与该子空间正交:

$$ \sum_{k}\xi_{k}^{\mu}\xi_{k}^{*} = 0,\quad \forall \mu = 1,2,\cdots,p $$

若 $w_{ik}$ 为一个解, 则 $w_{ik}^{\prime} = w_{ik} + a_{i}\xi_{k}^{*}$ 形成一个解系.

线性独立问题具有线性可分性, 反之则不同. 大多数阈值网络 $p>N$, 如 AND 和 XOR.

Gradient Descent Learning(梯度下降学习)

显式解允许我们直接求 $w_{ik}$, 但大多数情况下需要通过 learning rule 找到 $w_{ik}$.

评估误差的 Cost function:

$$ E[\vec{w}] = \frac{1}{2}\sum_{i\mu}(\zeta_{i}^{\mu} - O_{i}^{\mu})^{2} = \frac{1}{2}\sum_{i\mu}\left( \zeta_{i}^{\mu} - \sum_{k}w_{ik}\xi_{k}^{\mu} \right)^{2} $$

当 $E[\vec{w}] = 0$ 时找到解. 和依赖于节点激活的能量函数不同, 这里的函数依赖于权重/连接.

Gradient descent algorithm: 令 $w_{ik}$ 偏移 $\Delta w_{ik}$, 且幅度与梯度成正比:

$$ \begin{aligned} \Delta w_{ik} &= -\eta\frac{\partial E}{\partial w_{ik}} = \eta\sum_{\mu}(\zeta_{i}^{\mu}-O_{i}^{\mu})\xi_{k}^{\mu} \end{aligned} $$

$$ \begin{aligned} \frac{\partial E}{\partial w_{ik}} &= \frac{1}{2}\sum_{\mu}2\left( \zeta_{i}^{\mu} - \sum_{k}w_{ik}\xi_{k}^{\mu} \right)\cdot\frac{\partial}{\partial w_{ik}}\left( \zeta_{i}^{\mu} - \sum_{l}w_{il}\xi_{l}^{\mu} \right)\\ &= \sum_{\mu}\left( \zeta_{i}^{\mu} - \sum_{k}w_{ik}\xi_{k}^{\mu} \right)\cdot \left( -\sum_{l}\xi_{l}^{\mu}\delta_{lk} \right)\\ &= -\sum_{\mu}(\zeta_{i}^{\mu} - O_{i}^{\mu})\xi_{k}^{\mu} \end{aligned} $$

若固定模式 $\mu$, 则有 delta rule/adaline rule/Widrow-Hoff rule/Least Mean Squares (LMS) rule

$$ \Delta w_{ik} = \eta(\zeta_{i}^{\mu}-O_{i}^{\mu})\xi_{k}^{\mu} = \eta\delta_{i}^{\mu}\xi_{k}^{\mu} $$

Cost function 是一个二次型(quadratic form), 因此在 pattern subspace 形成抛物线面, 最小值即 $E=0$; 在正交于 subspace 的方向上 cost function 为常值.

${\xi_{k}^{\mu}}$ 线性相关时.

在对 $\vec{\xi}^{\mu}$ 学习后, 权重 $\vec{w}_{i} = (w_{i1},w_{i2},\cdots, w_{ik},\cdots,w_{iN})$ 只会在 $\vec{\xi}^{\mu}$ 的方向上变化, 而正交方向上不变.

Convergence of Gradient Descent

若 pattern vectors 线性无关, 则 cost function 写作

$$ E = \sum_{\lambda = 1}^{M}a_{\lambda}(w_{\lambda} - w_{\lambda}^{0})^{2} $$

$M$: 权重总数, 为输入节点数 $N$ 与输出节点数的乘积;

$w_{\lambda}$: $w_{ik}$ 的线性组合;

$a_{\lambda}$, $w_{\lambda}^{0}$: 依赖于模式矢量的常数. $a_{\lambda}$ 半正定(positive semi-definite); 当 $a_{\lambda} = 0$, $E$ 相当于对该 $\lambda$ 独立.

$$ \Delta w_{\lambda} = -\eta\frac{\partial E}{\partial w_{\lambda}} = -2\eta a_{\lambda}(w_{\lambda} - w_{\lambda}^{0}) = -2\eta a_{\lambda}\delta w_{\lambda} $$

那么定义辅助变量 $\delta w_{\lambda} = w_{\lambda} - w_{\lambda}^{0}$, 它表明到最优解的距离. 则原梯度下降规则的等式两边同减 $w_{\lambda}^{0}$ 得

$$ \delta w_{\lambda}^{\text{new}} = \delta w_{\lambda}^{\text{old}} + \Delta w_{\lambda} = (1-2\eta a_{\lambda})\delta w_{\lambda}^{\text{old}} $$

若 $|1-2\eta a_{\lambda}|<1$, 则可趋近最优点.

• $\eta<1/a_{\lambda}^{\text{max}}$
• $a_{\lambda}^{\text{min}}$ 决定收敛速度.

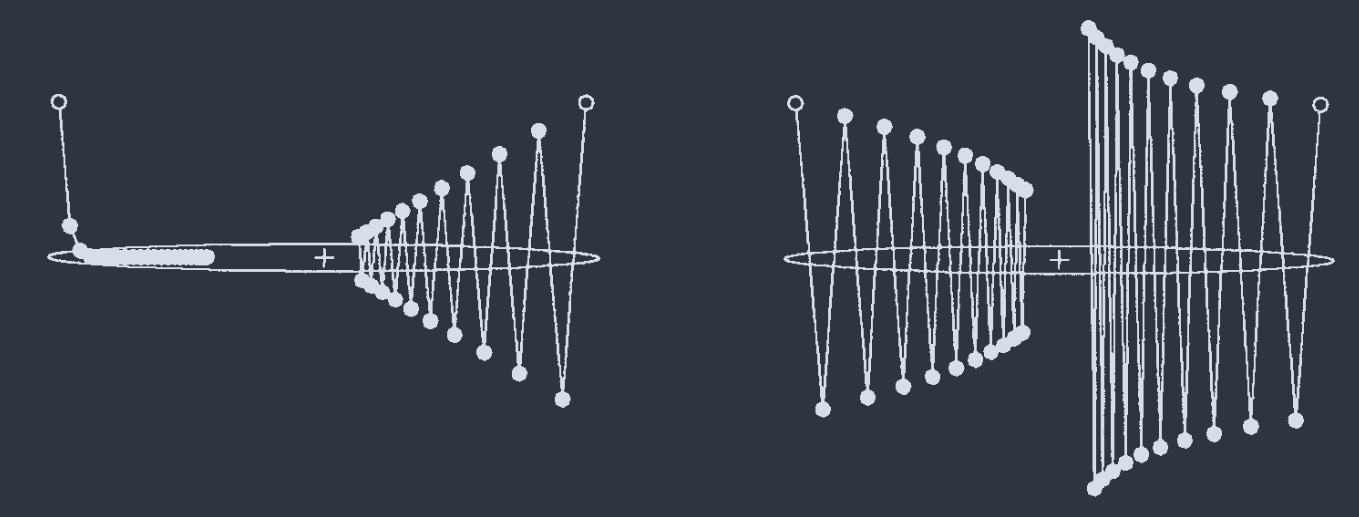
$E = x^{2} + 20 y^{2}$, $\eta = 0.02, 0.0476, 0.049, 0.0505$

在 patterns 存在线性相关组时, 则 cost function 改写为

$$ E = E_{0} + \sum_{\lambda=1}^{M}a_{\lambda}(w_{\lambda}-w_{\lambda}^{0})^{2},\quad E_{0}> 0 $$

5.5 Nonlinear Units

由线性 $g(h) = h$ 推广至任意可导 $g(h)$. Cost function:

$$ E[\vec{w}] = \frac{1}{2}\sum_{i\mu}(\zeta_{i}^{\mu} - O_{i}^{\mu})^{2} = \frac{1}{2}\sum_{i\mu}\left[ \zeta_{i}^{\mu} - g\left( \sum_{k}w_{ik}\xi_{k}^{\mu} \right) \right]^{2} $$

梯度

$$ \frac{\partial E}{\partial w_{ik}} = -\sum_{\mu}[\zeta_{i}^{\mu}-g(h_{i}^{\mu})]g^{\prime}(h_{i}^{\mu})\xi_{k}^{\mu} $$

权重修正

$$ \Delta w_{ik} = -\eta\frac{\partial E}{\partial w_{ik}} = \eta [\zeta_{i}^{\mu}-O_{i}^{\mu}]g^{\prime}(h_{i}^{\mu})\xi_{k}^{\mu} = \eta\delta_{i}^{\mu}\xi_{k}^{\mu} $$

对于 $g(h)=\tanh{(h)}$ 这类 sigmoid function, 在 $|h_{i}^{\mu}|$ 较小时梯度较大.

常用激活函数及其梯度: $$ \begin{aligned} \tanh{(h)} &= \frac{e^{h}-e^{-h}}{e^{h}+e^{-h}}\\ g(h)^{\prime} &= [\tanh{(\beta h)}]^{\prime} = \beta(1-g^{2});\\ f_{\beta}(h) &= \frac{1}{1+\exp{(-2\beta h)}}\\ g(h)^{\prime} &= f_{\beta}^{\prime}(h) = 2\beta g(1-g) \end{aligned} $$

解存在: patterns 线性无关.

梯度下降可能找到局部最优解(local minima) 而非全局最优解(global minima).

e.g. $g(h) = \tanh{(h)}$ 无法取到目标值 $\pm 1$.

Nonlinear units 在 patterns 线性相关时有可能辅助找到 partial solutions.

XOR problem.

$\xi_{1}$	$\xi_{2}$	$\zeta$
0	0	-1
0	1	+1
1	0	+1
1	1	-1

若取 $\tanh{(\beta h)}$ 作为激活函数:

• 最平凡的情况 $\vec{w} = \vec{0}$, 即 $O = 0$ 恒成立, 此时 $E = \frac{1}{2}[2\cdot (1-0)^{2}+2\cdot (-1-0)^{2}] = 2$.
• $|w_{0}|=|w_{1}|=|w_{2}|\rightarrow \infty$. 约定形式为 $h_{i}^{\mu} = w_{1}\xi_{1}+w_{2}\xi_{2} - w_{0}$; 若取符号为 $\{-,-,-\}$, 则 输出分别为 $\tanh{(0+0+\infty)} = +1$, $\tanh{(0-\infty+\infty)} = 0$, $\tanh{(-\infty+0+\infty)} = 0$, $\tanh{(-\infty-\infty+\infty)} = -1$. 此时 $E = \frac{1}{2}[(1+1)^{2}+(1-0)^{2}+(1-0)^{2}+0^{2}] = 3$??

Other Cost Functions

1. 对 $\zeta_{i}^{\mu}, O_{i}^{\mu}$ 可导; 2. 在 $O_{i}^{\mu} = \zeta_{i}^{\mu}$ 取最小值.

满足上述两要求均可成为 cost function.

$$ E = \sum_{i\mu}\left[ \frac{1}{2}(1+\zeta_{i}^{\mu})\log{\frac{1+\zeta_{i}^{\mu}}{1+O_{i}^{\mu}}} + \frac{1}{2}(1-\zeta_{i}^{\mu})\log{\frac{1-\zeta_{i}^{\mu}}{1-O_{i}^{\mu}}} \right] $$

在信息学中, 若有两个概率分布 $P(x)$ 和 $Q(x)$, 则 Relative entropy 被定义为 $$ D_{KL}(P||Q) = \sum_{x}P(x)\log{\frac{P(x)}{Q(x)}} $$

那么可以将 $\frac{1\pm O_{i}^{\mu}}{2}$ 理解为输出 $\pm 1$ 的概率, $\frac{1\pm \zeta_{i}^{\mu}}{2}$ 理解为实际目标为 $\pm 1$ 的概率.

当 $O_{i}^{\mu} = \zeta_{i}^{\mu}$ 时, $E=0$, 否则 $E>0$.

• 相比于二次型, 当 $|O_{i}^{\mu}|\rightarrow 1$ 时, 该 cost function 会发散, 从而推动网络修改权重. 二次型则是在 $|O_{i}^{\mu}|\rightarrow 1$ 时梯度趋近于 0, 导致学习停滞.
• 当训练集本身也是模糊的(如医药行业), 出身于概率论的 relative entropy cost function 更合适.

取 $g(h)=\tanh{\beta h}$ 作为激活函数, 则权重更新仍然为

$$ \Delta w_{ik} = \eta\delta_{i}^{\mu}\xi_{k}^{\mu},\quad \delta_{i}^{\mu} = {\color{red}{\beta}}(\zeta_{i}^{\mu}-O_{i}^{\mu}) $$

注意其中已经没有 $g^{\prime}(h_{i}^{\mu})$.

梯度下降:

• 用于二分决策问题(binary decision problems). $O_{i}>0$ 对应肯定, $O_{i}<0$ 对应否定;
• 适用于线性可分但 patterns 线性相关的问题;
• 使用 well-formed cost function, 如 relative entropy form, 其梯度幅值大于某定值, 从而总能找到解(如果解存在).

5.6 Stochastic Units

借助 Boltzmann 配分函数, 定义概率:

$$ P(S_{i}^{\mu}=+1) = \frac{e^{\beta h_{i}^{\mu}}}{e^{\beta h_{i}^{\mu}} + e^{-\beta h_{i}^{\mu}}},\quad P(S_{i}^{\mu}=-1) = \frac{e^{-\beta h_{i}^{\mu}}}{e^{\beta h_{i}^{\mu}} + e^{-\beta h_{i}^{\mu}}} $$

$$ h_{i}^{\mu} = \sum_{k}w_{ik}\xi_{k}^{\mu} $$

或者将其写作合并形式

$$ P(S_{i}^{\mu}=\pm 1) = \frac{1}{1+\exp{(\mp 2\beta h_{i}^{\mu})}} $$

于是得到

$$ \begin{aligned} \langle S_{i}^{\mu}\rangle &= (+1)\cdot \frac{e^{\beta h_{i}^{\mu}}}{e^{\beta h_{i}^{\mu}} + e^{-\beta h_{i}^{\mu}}} + (-1)\cdot \frac{e^{-\beta h_{i}^{\mu}}}{e^{\beta h_{i}^{\mu}} + e^{-\beta h_{i}^{\mu}}} \\ &= \tanh{(\beta h_{i}^{\mu})}\\ &= \tanh\left( \beta \sum_{k}w_{ik}\xi_{k}^{\mu} \right) \end{aligned} $$

权重更新

$$ \Delta w_{ik} = \eta\delta_{i}^{\mu}\xi_{k}^{\mu},\quad \delta_{i}^{\mu} = \zeta_{i}^{\mu} - \langle S_{i}^{\mu}\rangle $$

二次型 cost function:

$$ E = \frac{1}{2}\sum_{i\mu}(\zeta_{i}^{\mu} - S_{i}^{\mu})^{2} = \sum_{i\mu}(1-\zeta_{i}^{\mu}S_{i}^{\mu}) $$

$\zeta_{i}^{\mu},O_{i}^{\mu} = \pm 1$.

平均误差(avarage error):

$$ \langle E\rangle = \sum_{i\mu}(1-\zeta_{i}^{\mu}\langle S_{i}^{\mu}\rangle) = \sum_{i\mu}\left[ 1-\zeta_{i}^{\mu}\tanh{\left( \beta \sum_{k}w_{ik}\xi_{k}^{\mu} \right)} \right] $$

更新引起的 $\langle E\rangle$ 变化:

$$ \begin{aligned} \Delta\langle E\rangle &= \sum_{ik}\Delta w_{ik}\frac{\partial \langle E\rangle}{\partial w_{ik}}\\ &= \sum_{i\mu k}\Delta w_{ik}(-\zeta_{i}^{\mu})\frac{\partial }{\partial w_{ik}}\tanh{(\beta h_{i}^{\mu})}\\ &= -\sum_{i\mu k}\eta[1-\zeta_{i}^{\mu}\tanh{(\beta h_{i}^{\mu})}]\beta \text{ sech}^{2}(\beta h_{i}^{\mu})<0 \end{aligned} $$

所以更新总是改善平均表现.

Hints:

$$ \frac{\mathrm{d}}{\mathrm{d}x}\tanh{(x)} = \text{sech}^{2}(x),\quad \text{sech}(x) = \frac{1}{\cosh(x)} = \frac{2}{e^{x}+e^{-x}}\\ \frac{\partial}{\partial w_{ik}}\sum_{l}w_{il}\xi_{l}^{\mu} = \sum_{l}\xi_{l}^{\mu}\delta_{lk} = \xi_{k}^{\mu} $$

5.7 Capacity of the Simple Perceptron(简单感知机的容量)

• 可存储多少随机 input-output pairs?
• 通过特定学习规则, 多少 input-output pairs 可被学习?

continuous-valued units: 只要 $p$ 个 patterns 线性无关. 即 $p<N$. 因此容量 $p_{\text{max}} = N$.

threshold units: 要求线性可分性(是否存在超平面二分样本). 对于 random continous-valued inputs, $p_{\text{max}} = 2N$.

$N$ 通常为很大的 input units 数; output units 数很小且固定(不依赖于 $N$).

若给定 $p$ 个随机点于空间 $\mathbb{R}^{N}$ 中, 且其目标输出/标签随机分配为 $\pm 1$. 当 $p\leq 2N$ 时, 几乎总能找到一个超平面将其二分; 而当 $p>2N$ 时, 线性可分的概率迅速下降至 0.

每增加一个维度, 超平面都可以多分割两个点.

---

考虑 $N$ continous-valued inputs 和单个 $\pm 1$ output, 且 threshold 为 $0$(即 $N-1$ 维 hyperplane 过原点).

将 $p$ 个点随机放置于 $N$ 维空间, 且标签为 $\pm 1$. 令满足线性可分性的放置方法数为 $C(p,N)$.

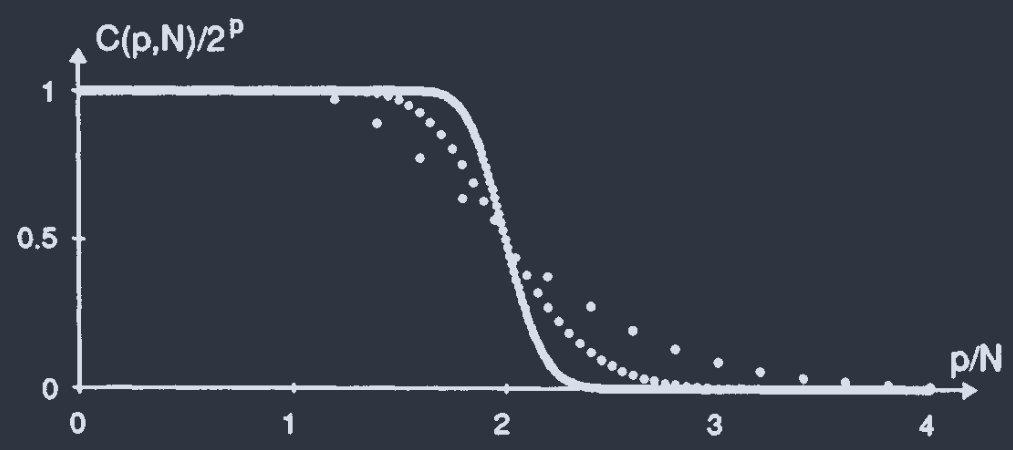
在 $p$ 很小时, $C(p,N)$ 可近似为 $2^{p}$, 即无论怎样染色都能找到一个超平面将其二分. $p$ 较大时, 开始出现线性不可分.

$N = \{\overset{\cdot}{5},\overset{\cdots}{20},\overset{-}{100}\}$. 在 $p/N = 2$ 时, $C(p,N)/2^{p}$ 急剧降低, 且 $N$ 越大, 跌落越快.

随机放置点不是必须的, 需要的是令其处于 general position(满足 linearly independent).

$N=2$, 即二维空间时, 线性无关要求两点连线不过原点.

dichotomy: 可被 hyperplane 二分的染色方法数.

在已有的 dichotomy 基础上添加第 $p+1$ 个点,

• 该点恰好位于 hyperplane 上, 则产生两个新 dichotomy, 因为无论将该点标记为 $+1$ 还是 $-1$, 都可以通过无限小偏移原 hyperplane 来实现二分;
• 只能标记为一种颜色, 否则将破坏线性可分性. 则新 dichotomy 对应于原旧 dichotomy.

$$ C(p+1,N) = C(p,N) + D $$

$D$ 是原 dichotomies 中 hyperplane 可同时穿过原点 $O$ 和新点 $P$ 的数量.

要求新点 $P$ 在原 hyperplane 上, 实际上就是多了一个约束条件 $\vec{w}\cdot\vec{\xi}^{P} = 0$, hyperplane 剩下的自由度只有 $N-1$, 而需要染色的点数仍然是 $p$ 个不变, 所以实际上 $D = C(p,N-1)$.

所有经过 $OP$ 的超平面集合 $\Leftrightarrow$ 在 $N-1$ 维空间中的所有超平面.

将原 $p$ 个点投影到正交于 $OP$ 的 $N-1$ 维子空间, 再考虑其线性分割.

这就形成了递推关系

$$ C(p+1,N) = C(p,N) + C(p, N-1) $$

迭代得到

$$ \begin{aligned} C(p,N) &= \begin{pmatrix} p-1\\ 0\end{pmatrix}C(1,N) + \begin{pmatrix} p-1\\ 1\end{pmatrix}C(1,N-1)+\cdots+\begin{pmatrix} p-1\\ p-1\end{pmatrix}C(1,N-p+1)\\ &= \sum_{j=0}^{p-1}\begin{pmatrix} p-1\\ j\end{pmatrix}C(1,N-j) \\ &= \sum_{j=0}^{p-1}C_{p-1}^{j}C(1,N-j) \end{aligned} $$

组合数 $$ \begin{pmatrix} m \\ n \end{pmatrix} = \frac{m!}{n!(m-n)!} = C_{m}^{n} $$

即从 $m$ 个不同元素中取出 $n$ 个元素($m>n$)的方法数.

使用归纳法证明.

1. 对于 $p=1$, 由于 $j\leq p-1$, 有意义的只有 $j = 0$ 项. 则等号右边

$$ C_{0}^{0}C(1,N) = 1\cdot C(1,N) $$

与等号左边 $C(1,N)$ 相等.

2. 假定 $p\geq 1$ 时结论成立, 则 $p+1$ 时, 验证

$$ \begin{aligned} C(p+1,N) &= C(p,N) + C(p,N-1)\\ &= \sum_{j=0}^{p-1}C_{p-1}^{j}C(1,N-j) + \sum_{j=0}^{p-1}C_{p-1}^{j}C(1,N-1-j)\\ k:=j+1\rightarrow &= \sum_{j=0}^{p-1}C_{p-1}^{j}C(1,N-j) + \sum_{k=1}^{p}C_{p-1}^{k-1}C(1,N-k)\\ &= C_{p-1}^{0}C(1,N) + \sum_{j=1}^{p-1}[C_{p-1}^{j}+C_{p-1}^{j-1}]C(1,N-j) + C_{p-1}^{p-1}C(1,N-p)\\ &= C_{p}^{0}C(1,N) + \sum_{j=1}^{p-1}C_{p}^{j}C(1,N-j) + C_{p}^{p}C(1,N-p)\\ &= \sum_{j=0}^{p}C_{p}^{j}C(1,N-j) \end{aligned} $$

正是取 $p+1$ 时的公式.

Pascal 恒等式

$$ C_{p}^{j} = C_{p-1}^{j} + C_{p-1}^{j-1} $$

即从 $p$ 个元素中选取 $j$ 个元素, 等效于先确定某固定特殊元素 $x$, 那么

1. 不含该元素, 即在剩下 $p-1$ 个元素中选取 $j$ 个元素, 即 $C_{p-1}^{j}$;
2. 一定要选取元素 $x$, 还有 $j-1$ 个元素没有选取, 并且要在剩下的 $p-1$ 个元素中选, 即 $C_{p-1}^{j-1}$.

• $p\leq N$: $\forall N$, $C(1,N)=2$, 因为一个点可以任意染色 $\pm 1$.
• $p>N$: 取 $N\leq 0$ 的 $C(p,N) = 0$.

所以公式中的 $C(1,N-j) = 2$. 代入得到

$$ C(p,N) = 2\sum_{i=0}^{N-1}C_{p-1}^{i} = 2\sum_{i=0}^{N-1}\begin{pmatrix} p-1\\ i \end{pmatrix} $$

当 $p = 2N$ 时, 利用二项式系数的对称性 $C_{2n}^{n-m} = C_{2n}^{n+m}$, 得到 $C(2N,N) = 2^{p-1}$. 和图中 $p/N = 2$ 时 $C(p,N)/2^{p} = 1/2$ 一致

在 $N$ 充分大时, 可将二项式系数处理为 Guassian 极限:

$$ \frac{C(p,N)}{2^{p}} \approx \frac{1}{2}\left[ 1 + \text{erf }\left( \sqrt{\frac{p}{2}}\left( \frac{2N}{p} - 1 \right) \right) \right] $$

证明:

$$ \frac{C(p,N)}{2^{p}} = \frac{2\sum_{i=0}^{N-1}C_{p-1}^{i}}{2^{p}} = \sum_{i=0}^{N-1}\frac{C_{p-1}^{i}}{2^{p-1}} = \text{Prob}(X\leq N-1) $$

注意到 $\begin{aligned} P(X = i) = C_{p-1}^{i}\left(\frac{1}{2}\right)^{p-1} \end{aligned}$, 则可引入二项分布 $X\sim B(p-1, 0.5)$.

$$ \langle X\rangle = \frac{1}{2}\cdot (p-1) = \frac{p-1}{2};\quad (\Delta X)^{2} = \langle X^{2}\rangle - \langle X\rangle^{2} = \frac{p-1}{4} $$

De Moivre–Laplace theorem

若 $X\sim B(n,p)$, 令 $\begin{aligned}z = \frac{x-\langle X\rangle}{\Delta X} = \frac{x-np}{\sqrt{np(1-p)}}\end{aligned}$. 当 $n\rightarrow \infty$:

• $\begin{aligned}P(X = x) = \frac{1}{\sqrt{np(1-p)}}\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}z^{2}}\end{aligned}$;
• $\begin{aligned}P(a\leq z\leq b) = \int_{a}^{b}\frac{1}{\sqrt{2\pi}}e^{-\frac{z^{2}}{2}}\mathrm{d}z\end{aligned}$.

定义 $\begin{aligned}\Phi(z) = \frac{1}{2}\left[1 + \text{erf}\left(\frac{z}{2}\right)\right]\end{aligned}$

$$ \begin{aligned} \frac{C(p,N)}{2^{p}} &\approx \Phi\left(\frac{(N-1)-\frac{p-1}{2}}{\sqrt{\frac{p-1}{4}}}\right)\approx \Phi\left(\frac{N - \frac{p}{2}}{\sqrt{\frac{p}{4}}}\right)\\ &= \frac{1}{2}\left\{ 1+ \text{erf}\left[\sqrt{\frac{p}{2}}\left( \frac{2N}{p} - 1 \right)\right] \right\} & \square \end{aligned} $$

Hopfield network 通过吸引子存储, 其不可相互干扰, 即稳定条件更严格. 因此 $\alpha_{c} \approx 0.138$ 相较于 perceptron 的要小的多.