The olfactory system of male moths is exquisitely sensitive to pheromones emitted by females and transported in the environment by atmospheric turbulence. Moths respond to minute amounts of pheromones, and their behavior is sensitive to the fine-scale structure of turbulent plumes where pheromone concentration is detectible. The signal of pheromone whiffs is qualitatively known to be intermittent, yet quantitative characterization of its statistical properties is lacking. This challenging fluid dynamics problem is also relevant for entomology, neurobiology, and the technological design of olfactory stimulators aimed at reproducing physiological odor signals in well-controlled laboratory conditions. Here, we develop a Lagrangian approach to the transport of pheromones by turbulent flows and exploit it to predict the statistics of odor detection during olfactory searches. The theory yields explicit probability distributions for the intensity and the duration of pheromone detections, as well as their spacing in time. Predictions are favorably tested by using numerical simulations, laboratory experiments, and field data for the atmospheric surface layer. The resulting signal of odor detections lends itself to implementation with state-of-the-art technologies and quantifies the amount and the type of information that male moths can exploit during olfactory searches.

雄性飞蛾的嗅觉系统对雌性释放的费洛蒙极为敏感，这些费洛蒙通过空气湍流在环境中传播。飞蛾对微量的费洛蒙有反应，其行为对湍流羽流中可检测到的费洛蒙浓度的细微结构非常敏感。费洛蒙气味信号被定性地认为是间歇性的，但其统计特性的定量描述仍然缺乏。这一具有挑战性的流体动力学问题对于昆虫学、神经生物学以及旨在在受控实验室条件下再现生理气味信号的嗅觉刺激器的技术设计也具有重要意义。在这里，我们开发了一种拉格朗日方法来研究湍流流动中费洛蒙的传输，并利用该方法预测了嗅觉搜索过程中气味检测的统计特性。该理论提供了关于费洛蒙检测强度和持续时间以及它们在时间上的间隔的明确概率分布。通过数值模拟、实验室实验和大气边界层的现场数据，对预测结果进行了有利的验证。所得到的气味检测信号可以使用最先进的技术实现，并量化了雄性飞蛾在嗅觉搜索过程中可以利用的信息量和类型。

INTRODUCTION

Sex pheromones provide arguably the most striking example of long-range communication through specialized airborne messengers. Most Lepidoptera are consistently attracted to calling females from distances going as far as several hundred meters, reaching their partners in a few minutes. This feat is impressive as females broadcast their pheromone message into a noise-ridden transmission medium (the turbulent atmospheric surface layer), and receiver males face the challenge of extracting information about the female’s location from a signal that is attenuated, garbled, and mixed with other olfactory stimuli (see Fig. 1).

性费洛蒙无疑是通过专门的空气信使进行远程通信的最显著例子。大多数鳞翅目昆虫会持续被呼唤的雌性吸引，距离可达数百米，并在几分钟内找到它们的伴侣。这一壮举令人印象深刻，因为雌性将其费洛蒙信息广播到一个充满噪音的传输介质（湍流大气边界层）中，而接收雄性面临着从一个被衰减、混乱并与其他嗅觉刺激混合的信号中提取有关雌性位置的信息的挑战（见图1）。

The pheromone communication system is under strong evolutionary pressure. This is particularly evident for adult moths of the family Saturniidae and Bombycidae (e.g., the Indian Luna and the silk moth, respectively), which have a lifespan of a few days as adults. Subsisting on stored lipids acquired during the larval stage, they largely devote their adulthood to the task of reproduction. The result of natural selection is an olfactory system exquisitely sensitive to pheromones: Just a few molecules impinging on the antenna of a male moth are sufficient to alert the insect and trigger a change in its cardiac frequency; concentrations of a few hundred molecules per cubic centimeter elicit specific behavioral responses that prelude flight.

费洛蒙通信系统承受着强大的进化压力。这在天蛾科和家蚕科的成虫中尤为明显（例如，印度月亮蛾和家蚕），它们作为成虫的寿命只有几天。它们依靠在幼虫阶段获得的储存脂质为生，主要将成年期用于繁殖任务。自然选择的结果是一个对费洛蒙极为敏感的嗅觉系统：只需少量分子撞击雄性飞蛾的触角，就足以警示昆虫并触发其心率变化；每立方厘米几百个分子的浓度会引发特定的行为反应，为飞行做准备。

The quality and the time course of the pheromone signal matter, in addition to its intensity. As for the quality, the signal is usually a blend of two or more chemical compounds. Species of closely related families often use similar components, and discrimination is achieved by different combinations and/or ratios in the mixture. Pheromone components of sympatric species that emit similar pheromone blends often act as behavioral antagonists, and the discrimination among different blends is extremely fine. The first-order center for the discrimination is the macroglomerular complex of the antennal lobe, where detections from olfactory receptor neurons are integrated. As for the time course of the signal, turbulence strongly distorts the pheromone signal, leading to wildly intermittent fluctuations of concentration at large distances from the source. As shown in Fig. 1, the signal features alternating bursts and clean-air periods with a broad spectrum of durations.

除了强度外，费洛蒙信号的质量和时间过程也很重要。就质量而言，信号通常是两种或更多化学成分的混合物。密切相关的物种通常使用类似的成分，而通过混合物中的不同组合和/或比例来实现区分。发出类似费洛蒙混合物的同域种的费洛蒙成分通常作为行为拮抗剂，不同混合物之间的区分非常细微。区分的一级中心是触角叶的宏球状复合体，在这里整合了来自嗅觉受体神经元的检测。就信号的时间过程而言，湍流强烈扭曲了费洛蒙信号，导致在距离源头较远处浓度出现极其间歇性的波动。如图 1 所示，该信号以交替出现的突发和清洁空气时期为特征，持续时间范围广泛。

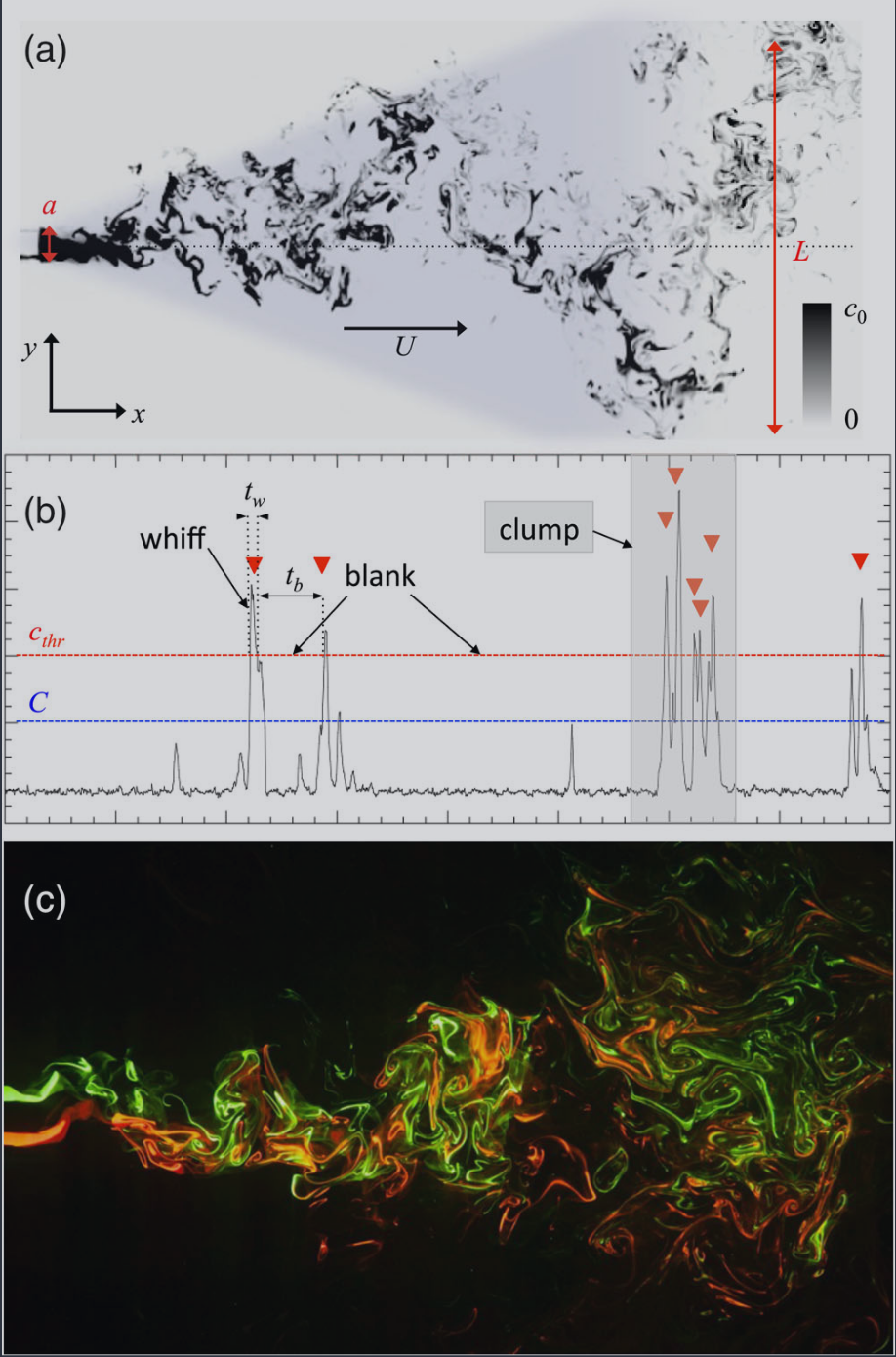
FIG. 1. The structure of a turbulent odor plume. (a) A twodimensional section of a plume from the jet-flow experiment. The shaded area is the projection of the conical average plume, i.e., the region outside of which crosswind transport is weak and the odor concentration decays rapidly. (b) A typical time series of the odor concentration at a given point in space. Red triangles indicate the occurrence of whiffs, i.e., intervals when the local concentration is above the threshold cthr indicated by the red line. For olfactory searches, the threshold is comparable to the sensitivity of the pheromone receptors of the insects. The blue line indicates the average concentration C in the regions where the signal is above the noise level. (c) A two-dimensional section of two blending plumes from the jet-flow experiment. The two different chemicals mix as they progress downwind, and the resulting signal is a blend.

图 1. 湍流气味羽流的结构。(a) 喷射流实验中羽流的二维截面。阴影区域是锥形平均羽流的投影，即横风输运较弱且气味浓度迅速衰减的区域之外。(b) 空间中给定点的气味浓度典型时间序列。红色三角形表示气味突发的发生，即局部浓度高于红线所示阈值 c_thr 的间隔。对于嗅觉搜索，阈值与昆虫费洛蒙受体的敏感性相当。蓝线表示信号高于噪声水平区域的平均浓度 C。(c) 喷射流实验中两个混合羽流的二维截面。两种不同的化学物质在下风处混合，产生的信号是混合物。

Characterizing the properties of odor detections in turbulent flows is a challenging and fundamental problem in statistical fluid dynamics. Furthermore, intermittency generated by the physics of turbulent transport is crucial for eliciting the appropriate biological behavior. Insects exposed to steady, uniform stimuli briefly move upwind, arrest their flight toward the source, and begin crosswind casting (the typical response to the loss of olfactory cues). Males temporarily resume upwind flight when the stimulus is increased stepwise, and they set into sustained upwind flight when exposed to repeated pulses. Hence, the statistics of turbulence-airborne odor stimuli is literally the message sent by female to male moths; it controls their behavior and defines the information that male moths can exploit for their searches. Therefore, the longstanding problem of characterizing the statistics of odor detections during olfactory searches is essential to understand the neurobiological response of insects. Additional motivation for considering the problem stems from laboratory experiments using olfactometers and/or tethering. Experiments in Refs. [19,20] have Drosophilae tethered to a wire and assay their responses (electrophysiologically and/or behaviorally) to simple odor stimuli, such as pulses of fixed duration, that are most likely not representative of those experienced in the wild. To determine the statistics of physiological stimuli and then reproduce it in the laboratory would represent major progress and would significantly impact the design of future experimental assays.

表征湍流中气味检测的特性是统计流体动力学中的一个具有挑战性和基础性的问题。此外，由湍流输运物理产生的间歇性对于引发适当的生物行为至关重要。暴露于稳定、均匀刺激下的昆虫会短暂地向上风移动，停止向源头飞行，并开始横风投掷（对失去嗅觉线索的典型反应）。当刺激逐步增加时，雄性会暂时恢复向上风飞行，并在暴露于重复脉冲时进入持续的向上风飞行。因此，湍流空气中气味刺激的统计数据实际上是雌性飞蛾发送给雄性飞蛾的信息；它控制着它们的行为，并定义了雄性飞蛾在搜索过程中可以利用的信息。因此，在嗅觉搜索过程中表征气味检测统计数据的长期问题对于理解昆虫的神经生物学反应至关重要。考虑这个问题的另一个动机来自使用嗅觉仪和/或系留的实验室实验。参考文献中的实验将果蝇系留在一根铁丝上，并测试它们对简单气味刺激（如固定持续时间的脉冲）的反应（电生理学和/或行为学），这些刺激很可能不代表它们在野外经历的刺激。确定生理刺激的统计数据并在实验室中再现它将代表重大进展，并将显著影响未来实验测定的设计。

Here, we address and answer the following questions: How intermittent is the distribution of pheromones as a function of the downwind or crosswind distance from the source? What are the statistical distributions for the intensity and the duration of odor-laden whiffs, and the duration of clean-air pockets? What is the dependency on the sensitivity threshold? How does turbulence affect the ratio among different components of a blend from emission to reception? Can emissions from multiple sources, with different blend ratios, reach the receiver without being irremediably mixed? Results are obtained by developing a theoretical Lagrangian approach that predicts the salient properties of a tracer emitted by a localized source and transported by a turbulent flow. We focus on a continuously emitting source, yet methods generalize to periodic emissions. Predictions are successfully tested by numerical simulations, and laboratory and field experimental data. Consequences for the neurobiological responses of insects during olfactory searches and for laboratory protocols of olfactory stimulation are discussed in the Conclusions.

在这里，我们解决并回答以下问题：费洛蒙的分布随着离源头的下风或横风距离变化有多间歇性？气味突发的强度和持续时间以及清洁空气口袋的持续时间的统计分布是什么？对敏感性阈值有什么依赖性？湍流如何影响从发射到接收的混合物中不同成分之间的比例？来自多个源、具有不同混合比例的排放能否在不被不可挽回地混合的情况下到达接收器？通过开发一种理论拉格朗日方法来预测由局部源发射并由湍流输送的示踪剂的显著特性，获得了结果。我们专注于连续发射源，但方法可以推广到周期性发射。通过数值模拟以及实验室和现场实验数据成功验证了预测结果。结论部分讨论了对昆虫在嗅觉搜索过程中的神经生物学反应以及嗅觉刺激实验室协议的影响。

THEORETICAL FRAMEWORK

Definition of the problem

We consider the emission by a source of linear size $a$ (at the origin $\vec{x}=\vec{0}$) of a chemical substance (or a mixture) at a constant rate of $J$ molecules per unit time. The environment transporting the chemical is a turbulent incompressible flow $\vec{u}(\vec{x},t) = \vec{U} + \vec{v}(\vec{x},t)$. The mean wind is $\vec{U} = (U,0,0)$, while $\vec{v}$ is the turbulent component. The turbulence level $v/U$, which is the ratio between the amplitudes of the turbulent component $\vec{v}$ and of the mean flow $\vec{U}$, is assumed to be small in the rest of the paper. We are interested in the time series of the concentration $c$ at a downwind distance $x$ (much larger than $a$ but still smaller than the correlation length $L$ of the flow) and crosswind distance $y$ from the source (see Fig. 1). The concentration $c(\vec{x},t)$ of the chemical obeys the advection-diffusion equation

$$ \frac{\partial c(\vec{x},t)}{\partial t} + \vec{u}(\vec{x},t) \cdot \nabla c(\vec{x},t) = \kappa\nabla^{2} c(\vec{x},t) + Jh_{a}(\vec{x}) $$

where $\kappa$ is the molecular diffusivity. The function $h_{a}(\vec{x})$ is the spatial distribution of the source of size $a$, e.g., a top hat vanishing outside the source ($|\vec{x}|>a$) and normalized to unity ($\int h_{a}(\vec{x})\mathrm{d}\vec{x} = 1$).

我们考虑一个线性尺寸为 $a$ 的源（位于原点 $\vec{x}=\vec{0}$）以恒定速率 $J$ 分子/单位时间发射化学物质（或混合物）。运输化学物质的环境是湍流不可压缩流 $\vec{u}(\vec{x},t) = \vec{U} + \vec{v}(\vec{x},t)$。平均风为 $\vec{U} = (U,0,0)$，而 $\vec{v}$ 是湍流分量。湍流等级 $v/U$，即湍流分量 $\vec{v}$ 和平均流 $\vec{U}$ 的幅度之比，在本文的其余部分中假设很小。我们感兴趣的是距离源头下风距离 $x$（远大于 $a$ 但仍小于流动的相关长度 $L$）和横风距离 $y$ 处的浓度 $c$ 的时间序列（见图 1）。化学物质的浓度 $c(\vec{x},t)$ 遵循对流扩散方程

$$ \frac{\partial c(\vec{x},t)}{\partial t} + \vec{u}(\vec{x},t) \cdot \nabla c(\vec{x},t) = \kappa\nabla^{2} c(\vec{x},t) + Jh_{a}(\vec{x}) $$

其中 $\kappa$ 是分子扩散率。函数 $h_{a}(\vec{x})$ 是尺寸为 $a$ 的源的空间分布，例如，在源外部（$|\vec{x}|>a$）消失并归一化为单位（$\int h_{a}(\vec{x})\mathrm{d}\vec{x} = 1$）的顶帽函数。

Quantities of interest.

We derive below the expression for the following observables of the concentration field $c$ at a given spatial location (see Fig. 1): (i) the intermittency coefficient $\chi$ defined as the fraction of time the concentration is nonzero. The smaller this number, the longer the searching insect is exposed to clean air. (ii) Next is the average concentration $C$ taken over periods of time when the signal is nonzero. The value of $C$ determines the typical intensity of concentration in an odor-laden plume and whether or not that level is detectible by the insect, as discussed below. (iii) Then, we have the full statistics of the signal intensity, that is, the probability distribution $p(c)$ of the concentration. Its expression involves $C$ and $\chi$ as fundamental parameters. (iv) Insects are supposed to detect a signal during those intervals of time when the local concentration exceeds some sensitivity threshold $c_{\text{thr}}$. We call those periods “whiffs,” while the complementary periods when $c\leq c_{\text{thr}}$ are dubbed “blanks,” or “below threshold.” The temporal structure of the signal is thus given by $p(t_{w})$, the probability distribution of the duration $t_{w}$ of the whiffs, and by $p(t_{b})$, the probability distribution of the duration tb of intervals below threshold, which we obtain below.

我们在下面推导了给定空间位置处浓度场 $c$ 的以下可观测量的表达式（见图 1）：(i) 间歇性系数 $\chi$，定义为浓度非零的时间比例。该数值越小，搜索昆虫暴露于清洁空气的时间就越长。(ii) 接下来是信号非零期间的平均浓度 $C$。$C$ 的值决定了气味羽流中浓度的典型强度，以及该水平是否可被昆虫检测到，如下所述。(iii) 然后，我们有信号强度的完整统计，即浓度的概率分布 $p(c)$。其表达式涉及 $C$ 和 $\chi$ 作为基本参数。(iv) 昆虫被假定在局部浓度超过某个敏感性阈值 $c_{\text{thr}}$ 的时间间隔内检测信号。我们将这些时期称为“气味突发”，而当 $c\leq c_{\text{thr}}$ 时的补充时期则称为“空白”或“低于阈值”。因此，信号的时间结构由气味突发持续时间 $t_{w}$ 的概率分布 $p(t_{w})$ 和低于阈值间隔持续时间 $t_{b}$ 的概率分布 $p(t_{b})$ 给出，我们将在下面获得这些分布。

The Lagrangian approach

Lagrangian methods (see Refs. [21–26] for introduction and reviews) focus on fluid-parcel trajectories, and the statistics of the concentration field is reconstructed from the properties of a suitable ensemble of trajectories. Lagrangian approaches are alternatives to the Eulerian description, where the main focus is the concentration field itself (as, e.g., in the fluctuating plume model). The two descriptions are formally equivalent, yet they lend themselves to physical approaches that are quite distinct. The Lagrangian reformulation of (1) is

$$ c(\vec{x},t) = J\int_{-\infty}^{t}\mathrm{d}t^{\prime}\int\mathrm{d}\vec{x}^{\prime}h_{a}(\vec{x}^{\prime})p_{v}(\vec{x}^{\prime},t^{\prime}|\vec{x},t) $$

where $p_{v}\mathrm{d}\vec{x}^{\prime}$ is the probability that a fluid parcel transported by the flow is around $\vec{x}^{\prime}$ at time $t^{\prime}$, given that it is in $\vec{x}$ at time $t$. The index of $p_{v}$ is meant to stress that the probability is averaged over the molecular noise statistics, but no average is taken over the fluctuating turbulent flow $\vec{v}$ (more details can be found in Ref. [26]). Equation (2) states that $c(\vec{x},t)$ is determined by tracing back in time the trajectories of parcels that end in $\vec{x}$ at time $t$. The ensemble of those trajectories forms a puff whose center of mass recedes upwind and whose size $r(t^{\prime})$ typically grows as $t^{\prime}\to -\infty$ (see Fig. 2). Depending on the realizations of $v$, two cases can be distinguished: (i) The distance between the center of mass of the puff and the source never becomes smaller than the size of the puff. These are pockets of clean air, where the concentration $c(\vec{x},t)$ vanishes, as follows from Eq. (2). (ii) Otherwise, the concentration $c(\vec{x},t)$ is nonvanishing.

拉格朗日方法（介绍和综述见参考文献）侧重于流体包裹体的轨迹，并从适当的轨迹集合的属性中重建浓度场的统计数据。拉格朗日方法是欧拉描述的替代方法，后者主要关注浓度场本身（例如，在波动羽流模型中）。这两种描述在形式上是等价的，但它们适用于截然不同的物理方法。方程（1）的拉格朗日重述为

$$ c(\vec{x},t) = J\int_{-\infty}^{t}\mathrm{d}t^{\prime}\int\mathrm{d}\vec{x}^{\prime}h_{a}(\vec{x}^{\prime})p_{v}(\vec{x}^{\prime},t^{\prime}|\vec{x},t) $$

其中 $p_{v}\mathrm{d}\vec{x}^{\prime}$ 是流体包裹体在时间 $t^{\prime}$ 被流动运输到 $\vec{x}^{\prime}$ 附近的概率，前提是它在时间 $t$ 位于 $\vec{x}$。$p_{v}$ 的下标旨在强调该概率是对分子噪声统计进行平均的，但没有对波动湍流流 $\vec{v}$ 进行平均（更多细节见参考文献）。方程（2）指出，$c(\vec{x},t)$ 是通过追溯在时间 $t$ 结束于 $\vec{x}$ 的包裹体轨迹来确定的。这些轨迹的集合形成一个包裹体，其质心向上风方向后退，其大小 $r(t^{\prime})$ 通常随着 $t^{\prime}\to -\infty$ 而增长（见图 2）。根据 $v$ 的实现，可以区分两种情况：(i) 包裹体质心与源之间的距离从未小于包裹体的大小。这些是清洁空气口袋，其中浓度 $c(\vec{x},t)$ 消失，如方程（2）所示。(ii) 否则，浓度 $c(\vec{x},t)$ 非零。

It follows from Eq. (2) that the value $c(\vec{x},t)$ is proportional to the time of overlap between the puff and the source. The problem thus reduces to characterizing the statistics of the corresponding residence time. The turbulent flow that disperses the puff creates convoluted folds of local structures having some directions extended while others are contracted down to the diffusive scale $\eta$ of the scalar concentration field. The specific nature of those structures is determined by the signs of the Lyapunov exponents of the flow. Here, though, we are interested in the statistics of the residence time at the source, the size of which is $a\gg\eta$. Therefore, we physically expect that the small-scale structures of the puff are smoothed out by the integrals appearing in Eq. (2), affecting only constant factors that are not essential for the specific quantities discussed here. In particular, if we disregard constants of order unity, a sufficient characterization of the puffs should be provided by the dynamics of their center of mass and their overall size. We shall derive below the consequences of these physical assumptions and compare the resulting predictions to numerical and experimental data.

由方程（2）可知，值 $c(\vec{x},t)$ 与包裹体与源的重叠时间成正比。因此，问题简化为表征相应驻留时间的统计数据。分散包裹体的湍流流动会产生局部结构的复杂折叠，其中一些方向被延伸，而其他方向则被压缩到标量浓度场的扩散尺度 $\eta$。这些结构的具体性质由流动的 Lyapunov 指数的符号决定。然而，在这里，我们感兴趣的是在源处的驻留时间统计数据，其大小为 $a\gg\eta$。因此，我们在物理上预计，包裹体的小尺度结构通过出现在方程（2）中的积分被平滑掉，只影响与此处讨论的特定量无关的常数因子。特别是，如果我们忽略数量级为一的常数，则包裹体的动力学及其整体大小应该足以提供充分的表征。我们将在下面推导这些物理假设的后果，并将所得预测与数值和实验数据进行比较。

Lagrangian properties of the turbulent flow

We will show shortly that the statistics of odor stimuli for the problem defined above depends on the details of the turbulent flow transporting the pheromones via three exponents: $\alpha$, $\gamma$, and $\beta$. Power laws are typically observed in turbulent flows as a consequence of scale-invariance properties of fluid dynamical equations. The exponents that we define below are related, respectively, to the dynamics of single-particle, pair dispersion, and rate of growth of the size of a dispersing puff.

我们将很快展示，上述问题中气味刺激的统计数据取决于通过三个指数 $\alpha$、$\gamma$ 和 $\beta$ 传输费洛蒙的湍流流动的细节。由于流体动力学方程的尺度不变性特性，湍流中通常观察到幂律。我们在下面定义的指数分别与单粒子动力学、对分散和分散包裹体大小增长率有关。

(i) The exponent $\alpha$ controls the distance traveled by a single particle at short times $t$ as $(kt)^{1/\alpha}$, with $k$ constant. The crosswind width of the average plume, outside of which detections are rare, scales with the downwind distance $x$ as $x^{1/\alpha}$. In most physical cases, the mean wind gives the dominant contribution, so that $\alpha=1$, $k=U$, and the shape of the average plume is conical. However, for one special case discussed below (the Kraichnan flow), single-particle dispersion is dominated by diffusion at short enough times ($\alpha=2$), and the standard $Ut$ behavior holds only at longer times (yet smaller than those needed to reach the source).

(i) 指数 $\alpha$ 控制单个粒子在短时间 $t$ 内的运动距离，表现为 $(kt)^{1/\alpha}$，其中 $k$ 是常数。平均羽流的横风宽度（在该宽度之外检测很少）随着下风距离 $x$ 的变化比例为 $x^{1/\alpha}$。在大多数物理情况下，平均风贡献占主导地位，因此 $\alpha=1$，$k=U$，平均羽流的形状是锥形。然而，对于下面讨论的一个特殊情况（Kraichnan 流），单粒子扩散在足够短的时间内由扩散主导（$\alpha=2$），而标准的 $Ut$ 行为仅在较长时间内成立（但仍小于到达源所需的时间）。

(ii) The exponent $\gamma$ is related to the dispersion of a pair of particles as $(k^{\prime}t)^{1/\gamma}$, where $k^{\prime}$ is a constant. For the applications below, the relevant values are $\gamma = 2/3$, corresponding to the Richardson-Kolmogorov scaling, $\gamma = 2$ for ordinary diffusion and $\gamma = 1$ for ballistic separation.

(ii) 指数 $\gamma$ 与一对粒子的扩散有关，表现为 $(k^{\prime}t)^{1/\gamma}$，其中 $k^{\prime}$ 是常数。对于下面的应用，相关值为 $\gamma = 2/3$，对应于 Richardson-Kolmogorov 标度，$\gamma = 2$ 对应于普通扩散，$\gamma = 1$ 对应于弹道分离。

(iii) Finally, the exponent $\beta$ is defined by the scaling relation for the rate of growth $\zeta_{r,t}\equiv \frac{\mathrm{d}\log{r}}{\mathrm{d}t} = t^{-1}(k^{\prime}t/r^{\gamma})^{\beta}$ of a puff of size $r$ at time $t$ after its release. For homogeneous and stationary flow, $\beta = 1$ and $\zeta$ depends only on the size. However, if the flow is inhomogeneous, the dependency is more complicated. Namely, in the neutral atmospheric layer, the dynamics explicitly depends on the height; the height of particles released close to the ground grows linearly with time. Nonhomogeneous effects of the height are then conveniently accounted for via the dependency of $\zeta_{r,t}$ on the time $t$ since the release of the puff (we show below that $\beta = 2$ in this case). The consistency between the definitions of $\beta$ and $\gamma$ is easy to check: $\frac{\mathrm{d}r}{\mathrm{d}t} = r\zeta_{r}\sim k^{\prime}t^{\beta - 1}r^{1-\beta\gamma}$, and integration of the equation yields $r\sim (k^{\prime}t)^{1/\gamma}$ for any $\beta$.

(iii) 最后，指数 $\beta$ 通过标度关系定义，即在释放后时间 $t$ 内，尺寸为 $r$ 的包裹体的增长率 $\zeta_{r,t}\equiv \frac{\mathrm{d}\log{r}}{\mathrm{d}t} = t^{-1}(k^{\prime}t/r^{\gamma})^{\beta}$。对于均匀和稳定的流动，$\beta = 1$，且 $\zeta$ 仅依赖于大小。然而，如果流动是不均匀的，则依赖关系更为复杂。即，在中性大气层中，动力学明确依赖于高度；接近地面释放的粒子的高度随时间线性增长。然后，通过 $\zeta_{r,t}$ 对自包裹体释放以来的时间 $t$ 的依赖性，可以方便地考虑高度的非均匀效应（我们将在下面展示在这种情况下 $\beta = 2$）。$\beta$ 和 $\gamma$ 定义之间的一致性很容易检查：$\frac{\mathrm{d}r}{\mathrm{d}t} = r\zeta_{r}\sim k^{\prime}t^{\beta - 1}r^{1-\beta\gamma}$，并且该方程的积分对于任何 $\beta$ 都产生 $r\sim (k^{\prime}t)^{1/\gamma}$。

RESULTS: THEORY

In this section, we summarize the theoretical results about intensity and dynamics of the concentration signal. Derivations are detailed in Appendix A.

在本节中，我们总结了关于浓度信号强度和动态的理论结果。推导详见附录 A。

The intensity of the concentration signal

DISCUSSIONS AND CONCLUSIONS

We first consider the implications of our results for the olfactory response of insects. The detection region—where the message sent by female to male moths is least garbled by the turbulence transporting the pheromones—is defined by two conditions: (i) The whiffs of pheromones are sufficiently frequent [that is, the intermittency factor $\chi$ defined in Eq. (3) is not small], and (ii) the typical concentration $C$ in a whiff is detectible; i.e., its ratio $C/c_{\text{thr}}$ with respect to the detection threshold $c_{\text{thr}}$ is not negligible. Experimental measurements show that B. mori males respond to air streams containing as little as 200 molecules of bombykol per cm3, corresponding to a sensitivity threshold $c_{\text{thr}}\sim 10^{−18}$ M [6]. Measured rates for the emission of pheromones by female moths are of the order of a few picograms per second (see, e.g., Ref. [40]), which correspond to an emission rate $J\sim 10 \text{fmol}/s$ for a molecular weight of a few hundred Daltons, typical for most pheromones. The corresponding concentration at the source is $c_{0}\sim 1 \text{pM}$, for a mean wind $U\sim 1 \text{m/s}$ and a size a of the source of a few centimeters, as is typical for female moths.

我们首先考虑我们的结果对昆虫嗅觉反应的影响。检测区域——雌性飞蛾发送给雄性飞蛾的信息受到传输费洛蒙的湍流干扰最小的区域——由两个条件定义：(i) 费洛蒙的气味突发足够频繁[即方程（3）中定义的间歇性因子 $\chi$ 不小]，以及 (ii) 气味突发中的典型浓度 $C$ 可被检测到；即，其与检测阈值 $c_{\text{thr}}$ 的比率 $C/c_{\text{thr}}$ 不可忽略。实验测量表明，B. mori 雄性对含有每立方厘米仅 200 分子家蚕酮的气流有反应，对应于敏感性阈值 $c_{\text{thr}}\sim 10^{−18}$ M [6]。雌性飞蛾释放费洛蒙的测量速率约为每秒几皮克克拉姆（见例如参考文献 [40]），对应于发射速率 $J\sim 10 \text{fmol}/s$，分子量为几百道尔顿，这是大多数费洛蒙的典型值。对于平均风速 $U\sim 1 \text{m/s}$ 和源头尺寸为几厘米（这是雌性飞蛾的典型尺寸），源头处的相应浓度为 $c_{0}\sim 1 \text{pM}$。

The physiological parameters above can be inserted into the results for the atmospheric surface layer that we derived here and summarized in Eq. (13). We find that the detection region is a semiconical volume (with aperture angle controlled by the ratio between the intensity of turbulent fluctuations and the mean wind) that extends to downwind distances $x_{\text{thr}} \sim 10^{3} \text{m}$, in agreement with observations. Hundreds of meters away from the source, the most likely duration $\tau$ of the whiffs is a few milliseconds, which compares well to the shortest pulses detectible by moths. At those distances, whiffs tend to occur in clusters, and a time window of 1 second centered around a detection typically contains 10–20 odor encounters. This informationridden pattern of stimulation is time integrated at the level of the projection neurons and plays an important role in enhancing the behavioral sensitivity and in promoting exploitative sustained upwind flight. Upon approaching the source while staying inside the detection cone, the duration of the clumps decreases proportionally to the distance to the source. As a result, the search process is expected to lead to a statistically self-similar set of flight trajectories. Outside the detection cone, periods without any detection of pheromones are typically much longer than the whiffs. Note that even inside the detection cone, periods below threshold might be very long and last up to hundreds of seconds.

上述生理参数可以插入我们在此处推导并在方程（13）中总结的大气表面层结果中。我们发现检测区域是一个半锥形体积（开口角由湍流波动强度与平均风速之比控制），延伸到下风距离 $x_{\text{thr}} \sim 10^{3} \text{m}$，这与观察结果一致。距离源头数百米处，气味突发的最可能持续时间 $\tau$ 为几毫秒，这与飞蛾可检测到的最短脉冲相当。在这些距离处，气味突发往往成簇出现，并且围绕检测的 1 秒时间窗口通常包含 10-20 次气味遭遇。这种充满信息的刺激模式在投射神经元水平上进行时间积分，在增强行为敏感性和促进利用性持续向上风飞行方面起着重要作用。在接近源头时，同时保持在检测锥内，簇的持续时间与到源头的距离成比例减少。因此，搜索过程预计会导致一组统计自相似的飞行轨迹。在检测锥外，通常没有任何费洛蒙检测的时期远长于气味突发。请注意，即使在检测锥内，低于阈值的时期也可能非常长，持续时间可达数百秒。

Moths switch to exploratory casting when detections become too sporadic (see, e.g., Ref. [43]). While surges are straightforward to define as upwind motion, the trajectories during casting phases are more involved. For example, the angle of flight with respect to the mean wind, the duration of crosswind extensions, and their dependencies on the duration of the ongoing blank period are all factors that potentially affect the patterns of flight during the casting phases. In particular, the extent of the memory of past detections that affect the casting is an open issue. Another open issue is whether or not spatial information on the location of previous detections is involved in the control of the casting (and how, if positive). Search strategies for olfactory robots (see Refs. [44,45]) have shown that extended temporal memory and maps of space do lead to effective searches that alternate surges and casting phases qualitatively resembling those of insects. However, neurobiological constraints were not considered. The upshot is that quantitative data on flight patterns and their relation to the history of detections are needed to make progress on the decision-making processes controlling the casting of insects during their olfactory searches.

昆虫在检测变得过于零散时会切换到探索性捕捉（见例如参考文献 [43]）。虽然上风运动可以直观地定义为冲刺，但投掷阶段的轨迹更为复杂。例如，相对于平均风的飞行角度、横风延伸的持续时间以及它们对正在进行的空白期持续时间的依赖性，都是可能影响投掷阶段飞行模式的因素。特别是，影响投掷的过去检测记忆的范围是一个悬而未决的问题。另一个悬而未决的问题是，是否涉及先前检测位置的空间信息来控制投掷（如果是的话，如何控制）。嗅觉机器人的搜索策略（见参考文献 [44,45]）表明，扩展的时间记忆和空间地图确实导致了有效的搜索，这些搜索交替进行冲刺和投掷阶段，在质量上类似于昆虫。然而，没有考虑神经生物学约束。结果是，需要关于飞行模式及其与检测历史关系的定量数据，以推动控制昆虫在嗅觉搜索过程中投掷的决策过程的发展。

Laboratory bioassays with olfactometers and tethered insects are poised to shed light on the previous issues by jointly analyzing the time history of odor stimuli and the virtual flight trajectories of the insects. To ensure that responses observed in the laboratory are informative about the actual behavior of insects, though, it is crucial that stimuli be as close as possible to those experienced by insects in the open field. This is the practical level where our results will be useful: Equations (3)–(6) define a complete protocol for generating a sequence of odor pulses. The generation of such stimuli for the neutral atmospheric boundary layer seems achievable mechanically (see Refs. [19,20]) or optogenetically [41], i.e., opening or closing valves that control the delivery of odors or switching on or off light stimulation. For the former, some care should be taken in controlling adsorption effects. It is indeed known that they can lead to delays in the stimulation (see, e.g., Ref. [46]) that could prevent reproducing fast frequencies in the few-ms range that are predicted by Eqs. (5) and (6). No additional stringent limitations seem to prevent reproducing the statistics of Eqs. (3)–(6) in the laboratory. Trains of odor stimuli having such distributions will provide a statistically faithful representation of the landscape of odor detections created by atmospheric turbulence during olfactory searches. The protocol we derived here should then inform the design of future olfactory stimulation assays.

实验室使用嗅觉仪和系留昆虫的生物测定有望通过联合分析气味刺激的时间历史和昆虫的虚拟飞行轨迹来阐明前面的问题。然而，为了确保在实验室中观察到的反应对昆虫的实际行为具有信息性，至关重要的是，刺激应尽可能接近昆虫在开放环境中经历的刺激。这是我们的结果将有用的实际层面：方程（3）–（6）定义了生成一系列气味脉冲的完整协议。为中性大气边界层生成此类刺激似乎可以通过机械方式实现（见参考文献 [19,20]）或通过光遗传学方式实现 [41]，即打开或关闭控制气味传递的阀门或开启或关闭光刺激。对于前者，应注意控制吸附效应。确实已知它们可能导致刺激延迟（见例如参考文献 [46]），这可能会阻止再现方程（5）和（6）预测的几毫秒范围内的快速频率。似乎没有其他严格的限制阻止在实验室中再现方程（3）–（6）的统计数据。具有这种分布的气味刺激序列将提供大气湍流在嗅觉搜索过程中产生的气味检测景观的统计上真实的表示。我们在这里推导的协议应为未来嗅觉刺激测定的设计提供信息。