Integration—the accumulation of information over time—is a fundamental computation in navigation, decisionmaking, and memory. The dominant circuit model, the continuous attractor neural network (CANN), explains integration through finely tuned connectivity that supports marginally stable states.
However, data from systems such as Drosophila central complex suggest that real connectivity is heterogeneous, implying that symmetry may only exist in a coarse-grained sense, if at all. One class of models explains this heterogenous connectivity by evoking supervised learning which can enforce coarse-grained symmetry at the expense of extensive trial and error learning or by employing biologically unrealistic learning rules. Another class employs only local learning rules, but this approach typically fails when circuit connectivity or tutoring inputs become sufficiently heterogeneous.
积分——随时间积累信息——是导航、决策和记忆中的基本计算. 主导的回路模型, 连续吸引子神经网络(CANN), 通过支持边际稳定状态的精细调制连接来解释积分.
然而, 来自 果蝇 中央复合体等系统的数据表明, 真实的连接是异质的, 这意味着对称性可能仅以 粗粒化 的意义存在(如果存在的话). 一类模型通过提出 监督学习 来解释这种异质连接, 这可以以广泛的反复试验学习为代价来强制执行粗粒化对称性, 或者通过采用生物学上不现实的学习规则来实现. 另一类仅使用 局部学习规则, 但当回路连接或辅导输入变得足够异质时, 这种方法通常会失败.
Here, we attempt to bridge this gap by taking a machine learning approach (meta-learning) to identify local learning rules that can organize integration dynamics in heterogeneous networks.
The learned rule is parameterized as the Taylor expansion of an arbitrary function that depends on synapse size as well as eligibility traces of preand postsynaptic activity and input from other cell types.
在这里, 我们试图通过采用机器学习方法(元学习)来识别可以在异质网络中组织积分动态的局部学习规则来弥合这一差距.
学习规则被参数化为依赖于 突触 大小以及前突触和后突触活动的 资格迹 和其他细胞类型输入的任意函数的 Taylor 展开.
We discover rules that form bump attractors given only weak spatial priors and integration inputs.
In a simpler two-neuron system, we find rules that generate line attractor dynamics.
Shared features across both learned rules include anti-Hebbian spike-timing-dependent plasticity, in which synapses supporting sequential activity are depressed, and input-dependent potentiation.
我们发现了仅在弱空间先验和积分输入下形成突起吸引子的规则.
在一个更简单的双神经元系统中, 我们找到了产生线性吸引子动力学的规则.
两个学习规则之间的共同特征包括反 Hebbian 尖峰时序依赖性可塑性, 其中支持顺序活动的突触被抑制, 以及输入依赖性增强.
We find these common components underlie two different forms of plasticity rule:
the first, learned when the period of integration is short, causes weights to converge and drives the dynamics toward marginal stability.
Under the second, weights never converge, but are adjusted to move around a fixed point, maintaining memory. We recapitulate the latter rule in a simple system and show that it integrates effectively.
我们发现这些共同组成部分构成了两种不同形式的可塑性规则:
第一种, 在积分期较短时学习到, 导致权重收敛并推动动力学朝向边际稳定.
在第二种情况下, 权重从不收敛, 但被调整以围绕一个固定点移动, 从而保持记忆. 我们在一个简单系统中重新演绎了后者规则, 并展示了它有效地进行积分.
Integration is an essential part of many natural behaviors: for example, organisms might recall the amount of food they discover while foraging in a particular location or sum self-motion inputs to keep track of their heading.
While integration has previously been modeled as learned through feedback or tutoring inputs, here, we ask: can unsupervised local plasticity rules self-organize integration dynamics?
Integration has traditionally been thought to be difficult to learn without these supervised signals, since heterogeneity in attractor network properties, e.g. the strength of recurrent inhibition (Fig 1b-d), can cause a manifold of marginally stable states to bifurcate into a set of fixed points (Fig 1e).
积分是许多自然行为的重要组成部分: 例如, 有机体可能会回忆起它们在特定位置觅食时发现的食物量, 或者求和自我运动输入以跟踪它们的朝向.
虽然积分以前被建模为通过反馈或辅导输入学习, 但在这里, 我们问: 无监督的局部可塑性规则能否自组织积分动力学?
传统上认为, 没有这些监督信号, 积分很难学习, 因为吸引子网络属性中的异质性(例如递归抑制的强度(图 1b-d))可能导致边际稳定状态的流形分叉成一组固定点(图 1e).
We use a machine learning approach (meta-learning) to openendedly learn a set of local plasticity rules that facilitate integration.
We form a polynomial basis of terms dependent on factors like synapse size, pre- and postsynaptic activity, input current from a distinct cell types, as well as bounds on incoming and outgoing summed synaptic strength (Fig 1f). We search for rules capable of integrating transient input cues.
Networks are simulated for 400 epochs in which they receive right and left input cues, with the aim of outputting the integrated difference of these signals (Fig 1a; Fig 2a).
In the last 120 epochs, we assume plasticity has driven weights to converge upon a solution, and we construct a decoder that reads out an integrated value from network activity. The efficacy with which this decoder can read out integrated cues on future trials is then used to define the loss of the plasticity rule within the meta-learning procedure. We then iteratively tune the plasticity rules to minimize this supervised loss (Fig 1g).
我们使用 机器学习方法(元学习) 来开放式地学习一组促进积分的局部可塑性规则.
我们形成了一个依赖于突触大小、前突触和后突触活动、来自不同细胞类型的输入电流以及传入和传出总突触强度边界等因素的多项式基(图 1f). 我们寻找能够积分瞬时输入线索的规则.
网络在 400 个时期内进行模拟, 在此期间它们接收"左"/“右"输入线索, 目标是输出这些信号的积分差(图 1a;图 2a).
在最后 120 个时期中, 我们假设可塑性已将权重驱动到收敛于一个解决方案, 并且我们构建了一个解码器, 从网络活动中读出一个集成值. 该解码器在未来试验中读取集成线索的效率然后用于在元学习过程中定义可塑性规则的 loss. 然后我们迭代调整可塑性规则以最小化这种监督 loss(图 1g).
We learn rules in two different settings: the first reflects connectivity in the central complex of Drosophila (Fig 1a), the second is a 3-neuron system (2 excitatory, 1 inhibitory; Fig 2g).
Our closed-loop search uncovers sets of plasticity rules that robustly organize both types of network into integrators. Rules perform well at integration tasks extending up to 1 second, even when recurrent inhibitory connections are made heterogeneous (Fig 2d).
In central complex-like networks, one cell type learns to maintain a bump of activity that is steered around by incoming inputs from the other cell type (Fig 1b). Sampled tuning curves from the evolved system reflect a continuum of encoding states (Fig 2c).
我们在两种不同的设置中学习规则: 第一种反映了果蝇中央复合体中的连接性(图 1a), 第二种是一个 3 神经元系统(2 个兴奋性, 1 个抑制性;图 2g).
我们的闭环搜索发现了一组可塑性规则, 可以将这两种类型的网络稳健地组织成积分器. 即使递归抑制连接变得异质, 规则在扩展到 1 秒的积分任务中表现良好(图 2d).
在类似中央复合体的网络中, 一种细胞类型学会维持一个活动突起, 该突起由来自另一种细胞类型的输入引导(图 1b). 从进化系统中采样的调谐曲线反映了一系列编码状态(图 2c).
We investigated the learned rules by probing them with delta function inputs of varying amplitudes.
Learned rules in both systems contained core common features: a timingdependent anti-Hebbian rule, predicted by Xie and Seung [1999] and Hahnloser [2003], which converts into a symmetric, potentiating kernel when integration input from cell type 2 is present (Fig 2e).
We find that the nature of the learned rules changes in character as the length of the integration period grows. For short integration periods, rules organize approximate line attracting dynamics in which the weights largely converge and the network achieves marginal stability (Fig 2f).
When the integration period is long, weights do not converge, and networks do not possess marginal stability. However, plasticity in this regime still facilitates integration by rapidly and continuously moving a fixed point about a manifold of possible fixed point locations (Fig 1h), implementing memory that is partially synaptic.
We reproduce this idea in a model of two neurons (similar to Fig 1g). We find that with the addition of a bound on summed strength of synapses exiting a neuron, the fixed point can be constrained to a predictable manifold (Fig 2i), and the plasticity rules can facilitate integration (Fig 2j).
我们通过用不同幅度的 delta 函数输入探测它们来研究学习到的规则.
两个系统中学习到的规则都包含核心共同特征: 一种时序依赖的反 Hebbian 规则, 由 Xie 和 Seung [1999] 以及 Hahnloser [2003] 预测, 当来自细胞类型 2 的积分输入存在时, 该规则转换为对称的增强内核(图 2e).
我们发现, 随着积分期长度的增长, 学习规则的性质发生了变化. 对于较短的积分期, 规则组织了近似线性吸引动力学, 其中权重大部分收敛, 网络实现了边际稳定性(图 2f).
当积分期较长时, 权重不会收敛, 网络也不具备边际稳定性. 然而, 这一机制中的可塑性仍然通过快速且持续地在可能的固定点位置流形上移动固定点来促进积分(图 1h), 实现部分突触记忆.
我们在一个双神经元模型中复现了这个想法(类似于图 1g). 我们发现, 通过添加对离开神经元的突触总强度的约束, 可以将不动点限制在一个可预测的流形上(图 2i), 并且可塑性规则可以促进积分(图 2j).
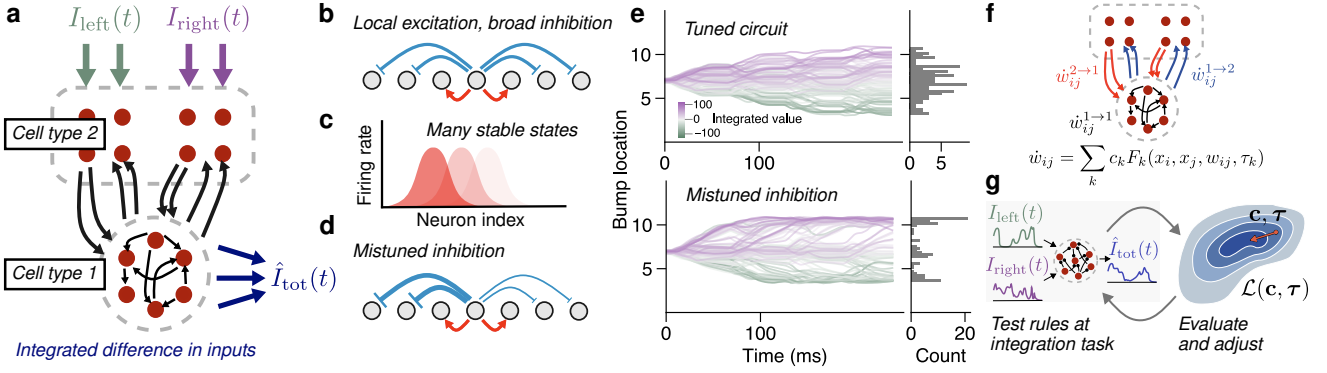
Figure 1: Learning plasticity rules that antagonistically integrate inputs using meta-learning (a) A central complex-like network receives right and left inputs, the integrated difference of which is the target output of cell type 2. (b) Typically integration is explained by continuous attractor networks, which use local excitation and global inhibition to maintain a manifold of marginally stable states (c). (d) Mistuning causes integration behavior to deteriorate (e). (f) We meta-learn a set of unsupervised plasticity rules that act on synapses within the circuit using only local information: preand postsynaptic activity $(x_j , x_i)$, eligibility traces of these activities, regulated by time constants ($\tau$), synapse size ($w_{ij}$), and input current from other cell types. (g) Coefficients and time constants are iteratively tuned.
图 1: 使用元学习学习对抗性积分输入的可塑性规则
(a) 类似中央复合体的网络接收左右输入, 其集成差异是细胞类型 2 的目标输出.
(b) 通常, 积分通过连续吸引子网络来解释, 该网络使用局部兴奋和全局抑制来维持边际稳定状态的流形 (c).(d) 调整错误会导致积分行为恶化
(e).(f) 我们元学习一组无监督的可塑性规则, 这些规则仅使用局部信息作用于电路内的突触: 前突触和后突触活动 $(x_j , x_i)$、这些活动的资格迹, 由时间常数 ($\tau$)、突触大小 ($w_{ij}$) 和来自其他细胞类型的输入电流调节.
(g) 迭代调整系数和时间常数.
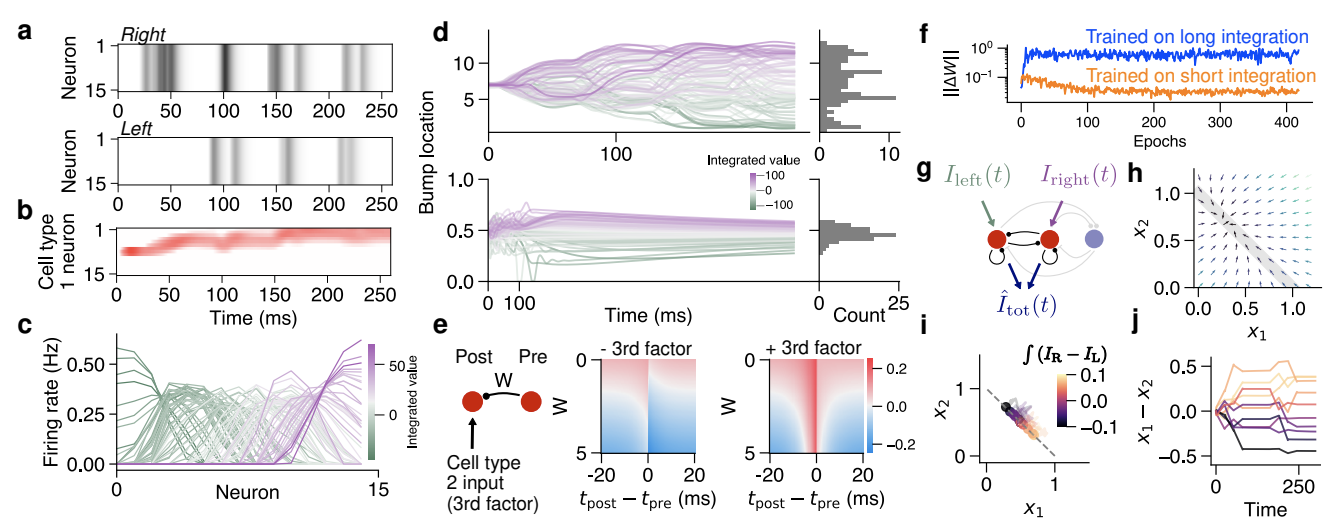
Figure 2: Discovered rules faithfully organize integrators in a central complex-like circuit and simplified 3-neuron system (a) Example right and left inputs, which are delivered to distinct populations in cell type 2 (see Fig 1a). (b) Learned rules cause cell type 1 to track integrated inputs with a bump of activity. (c) Tuning curves of neurons in cell type 1 reflect a continuum of states. (d) Tracking the peak of the activity bump over many trials in the Drosophila network (top). Traces from the 3-neuron network integrating and holding inputs (bottom). (e) Synaptic weight change as a function of synapse size and timing between pre- and postsynaptic neurons for synapses between cell type 1 neurons. Recent input from cell type 2 converts anti-Hebbian kernel into symmetric potentiation. (f) Rules learned on long integration periods tend not to cause weights to converge when compared with weights learned on short integration periods. (g) The 3-neuron model. Two excitatory neurons receive right and left inputs and are inhibited by mutual, global inhibition. (h) Illustrative flow field for rules that continually change weights. A fixed point can be moved about a manifold of possible locations to maintain memory. (i) A simplified model containing anti-Hebbian plasticity, input potentiation, and a presynaptic bound can integrate and its activity states are constrained to a manifold. (j) Integrated traces over time for model in (i).
图 2: 发现的规则忠实地组织了类似中央复合体电路和简化的 3 神经元系统中的积分器
(a) 示例右输入和左输入, 分别传递给细胞类型 2 中的不同群体(见图 1a).
(b) 学习到的规则使细胞类型 1 通过活动突起跟踪集成输入.
(c) 细胞类型 1 中神经元的调谐曲线反映了一系列状态.
(d) 在果蝇网络中跟踪许多试验中活动突起的峰值(顶部). 3 神经元网络集成和保持输入的轨迹(底部).
(e) 细胞类型 1 神经元之间突触的突触大小和前后突触神经元之间时序作为函数的突触权重变化. 来自细胞类型 2 的近期输入将反 Hebbian 核转换为对称增强.
(f) 与在短积分期上学习到的权重相比, 在长积分期上学习到的规则往往不会导致权重收敛.
(g) 3 神经元模型. 两个兴奋性神经元接收左右输入, 并通过相互全局抑制受到抑制.
(h) 持续改变权重的规则的说明性流场. 可以在可能位置的流形上移动固定点以保持记忆.
(i) 包含反 Hebbian 可塑性、输入增强和突触前界限的简化模型可以进行积分, 其活动状态被限制在一个流形上.
(j) (i) 中模型随时间集成的轨迹.