The Royal Swedish Academy of Sciences has decided to award the Nobel Prize in Physics 2024 jointly to John J. Hopfield and Geoffrey Hinton “for foundational discoveries and inventions that enable machine learning with artificial neural networks”.
瑞典皇家科学院决定将 2024 年诺贝尔物理学奖联合授予约翰-霍普菲尔德(John J. Hopfield)和杰弗里-辛顿(Geoffrey Hinton),“以表彰他们利用人工神经网络实现机器学习的奠基性发现和发明”。
Introduction
With its roots in the 1940s, machine learning based on artificial neural networks (ANNs) has developed over the past three decades into a versatile and powerful tool, with both everyday and advanced scientific applications. With ANNs the boundaries of physics are extended to host phenomena of life as well as computation.
起源于 20 世纪 40 年代的基于 人工神经网络(ANN) 的机器学习,在过去的三十年中发展成为一种多功能且强大的工具,既有日常应用,也有先进的科学应用。通过人工神经网络,物理学的边界得以扩展,以容纳生命现象和计算现象。
Inspired by biological neurons in the brain, ANNs are large collections of “neurons”, or nodes, connected by “synapses”, or weighted couplings, which are trained to perform certain tasks rather than asked to execute a predetermined set of instructions. Their basic structure has close similarities with spin models in statistical physics applied to magnetism or alloy theory. This year’s Nobel Prize in Physics recognizes research exploiting this connection to make breakthrough methodological advances in the field of ANN.
受大脑中生物神经元的启发,人工神经网络是由大量“神经元”或节点组成的集合,这些节点通过“突触”或加权耦合连接在一起,经过训练以执行特定任务,而不是执行预定的指令集。它们的基本结构与应用于磁学或合金理论的统计物理中的自旋模型有着密切的相似性。今年的诺贝尔物理学奖表彰了利用这种联系在人工神经网络领域取得突破性方法进展的研究。
Historical background
The first electronic-based computers appeared in the 1940s, and were invented for military and scientific purposes. They were intended to carry out computations that were cumbersome and time-consuming for humans. In the 1950s, the opposite need emerged, namely to get computers to do what humans and other mammals are good at – pattern recognition.
20 世纪 40 年代出现了第一批基于电子的计算机,最初是为军事和科学目的而发明的。它们旨在执行对人类来说繁琐且耗时的计算。20 世纪 50 年代,出现了相反的需求,即让计算机能够完成那些人类和其他哺乳动物擅长的任务——模式识别。
This artificial intelligence-oriented objective was first approached by mathematicians and computer scientists, who developed programs based on logical rules. This approach was pursued until the 1980s, but the computational resources that were required for the exact classifications, for example, of images became prohibitive.
这一面向人工智能的目标最初由数学家和计算机科学家提出,他们开发了基于逻辑规则的程序。这种方法一直持续到 20 世纪 80 年代,但所需的计算资源变得过于庞大,例如对图像进行精确分类。
In parallel, efforts had been initiated to find out how biological systems solve the pattern recognition problem. As early as 1943, Warren McCulloch and Walter Pitts, a neuroscientist and a logician, respectively, had proposed a model for how the neurons in the brain cooperate. In their model, a neuron formed a weighted sum of binary incoming signals from other neurons, which determined a binary outgoing signal. Their work became a launch pad for later research into both biological and artificial neural networks.
与此同时,人们开始努力研究生物系统如何解决模式识别问题。早在 1943 年,神经科学家 Warren McCulloch 和逻辑学家 Walter Pitts 就提出了一个关于大脑中神经元如何协作的模型。在他们的模型中,神经元对来自其他神经元的二进制输入信号进行加权求和,从而决定输出的二进制信号。他们的工作成为后续生物和人工神经网络研究的起点。
Another influential early contribution came from the psychologist Donald Hebb. In 1949, Hebb proposed a mechanism for learning and memories, where the simultaneous and repeated activation of two neurons leads to an increased strength of the synapse between them.
另一项有影响力的早期贡献来自心理学家 Donald Hebb。1949 年,Hebb 提出了一种学习和记忆机制,即两个神经元的同时和反复激活会导致它们之间突触强度的增加。
In the ANN area, two architectures for systems of interconnected nodes were explored, “recurrent” and “feedforward” networks, where the former allows for feedback interactions (Figures 1 and 2). A feedforward network has input and output layers and may also contain additional layers of hidden nodes sandwiched in-between.
在人工神经网络领域,探索了两种互连节点系统的架构:“递归”和“前馈”网络,前者允许反馈交互(图 1 和图 2)。前馈网络具有输入层和输出层,并且可能包含夹在中间的隐藏节点的附加层。
In 1957, Frank Rosenblatt proposed a feedforward network for image interpretation, which was also implemented in computer hardware. It had three layers of nodes, with adjustable weights only between the middle and output layers. Those weights were determined in a systematic fashion.
1957 年,Frank Rosenblatt 提出了一种用于图像解释的前馈网络,并在计算机硬件中实现。它有三层节点,只有中间层和输出层之间的权重是可调的。这些权重是以系统化的方式确定的。
Rosenblatt’s system attracted considerable attention, but it had limitations when it came to nonlinear problems. A simple example is the “one or the other but not both” (XOR) problem. These limitations were pointed out in an influential book by Marvin Minsky and Seymour Papert in 1969, which led to a hiatus funding-wise for ANN research.
Rosenblatt 的系统引起了广泛关注,但在处理非线性问题时存在局限性。一个简单的例子是“要么这个,要么那个,但不能同时是两个”(XOR)问题。这些局限性在 Marvin Minsky 和 Seymour Papert 于 1969 年出版的一本有影响力的书中被指出,这导致了人工神经网络研究资金的中断。
A parallel development took inspiration from magnetic systems, which were to create models for recurrent neural networks and investigate their collective properties.
由磁性系统的平行发展受到启发,创建了递归神经网络的模型并研究其集体属性。
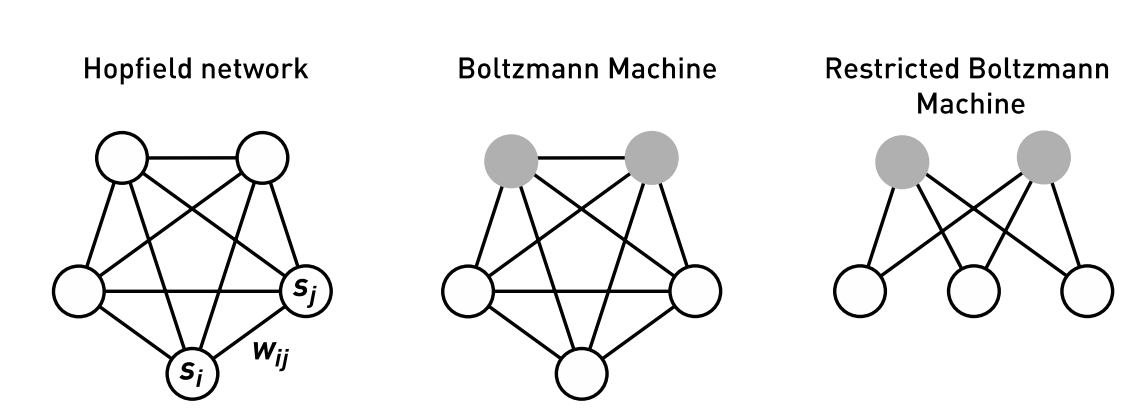
Recurrent networks of $N$ binary nodes $s_i$ (0 or 1), with connection weights $w_{ij}$. (Left) The Hopfield model. (Centre) Boltzmann machine. The nodes are divided into two groups, visible (open circles) and hidden (grey) nodes. The network is trained to approximate the probability distribution of a given set of visible patterns. Once trained, the network can be used to generate new instances from the learned distribution. (Right) Restricted Boltzmann Machine (RBM). Same as the Boltzmann machine, but without any couplings within the visible layer or between hidden nodes. This variant can be used for layer-by-layer pre-training of deep networks.
图 1. $N$ 个二进制节点 $s_i$(0 或 1)的递归网络,连接权重为 $w_{ij}$。(左)Hopfield 模型。(中)玻尔兹曼机。节点分为两组,可见节点(空心圆)和隐藏节点(灰色)。网络经过训练以近似给定可见模式集的概率分布。训练完成后,网络可以用来从学习到的分布中生成新实例。(右)受限玻尔兹曼机(RBM)。与玻尔兹曼机相同,但在可见层内或隐藏节点之间没有任何耦合。这种变体可用于深度网络的逐层预训练。
The 1980s
The 1980s saw major breakthroughs in the areas of both recurrent and feedforward neural networks, which led to a rapid expansion of the ANN field.
20 世纪 80 年代,递归神经网络和前馈神经网络领域都取得了重大突破,导致人工神经网络领域的快速扩展。
John Hopfield, a theoretical physicist, is a towering figure in biological physics. His seminal work in the 1970s examined electron transfer between biomolecules and error correction in biochemical reactions (kinetic proofreading).
理论物理学家 John Hopfield 是生物物理学领域的杰出人物。他在 20 世纪 70 年代的开创性工作研究了生物分子之间的电子转移和生化反应中的错误校正(动力学校对)。
In 1982, Hopfield published a dynamical model for an associative memory based on a simple recurrent neural network. Collective phenomena frequently occur in physical systems, such as domains in magnetic systems and vortices in fluid flow. Hopfield asked whether emergent collective phenomena in large collections of neurons could give rise to “computational” abilities.
1982 年,Hopfield 基于一个简单的递归神经网络发表了一个用于联想记忆的动态模型。集体现象在物理系统中经常发生,例如磁性系统中的畴和流体流动中的涡旋。Hopfield 询问大量神经元中出现的集体现象是否能够产生“计算”能力。
Noting that collective properties in many physical systems are robust to changes in model details, he addressed this question using a neural network with $N$ binary nodes $s_i$ (0 or 1). The dynamics were asynchronous with threshold updates of individual nodes at random times. The new value of a node $s_i$ was determined by a weighted sum over all other nodes,
$$ h_{i} = \sum_{j\neq i}w_{ij}s_{j}, $$
and was set to $s_i=1$ if $h_i>0$, and $s_i=0$ otherwise (with the threshold set to zero). The couplings $w_{ij}$ were assumed symmetric and to reflect pairwise correlations between the nodes in stored memories, which is referred to as the Hebb rule. The symmetry of the weights guarantees stable dynamics. Stationary states were identified as memories, distributed over the $N$ nodes in a nonlocal storage. Furthermore, the network was assigned an energy $E$ given by
$$ E = -\sum_{i<j}w_{ij}s_{i}s_{j} $$
which is a monotonically decreasing function under the dynamics of the network. Notable is that the connection between the world of physics, as defined in the 1980s, and ANNs was obvious already from these two equations. The first equation can be used to represent the Weiss molecular field (after the French physicist Pierre Weiss) that describes how atomic magnetic moments align in a solid, and the latter is often used to evaluate the energy of a magnetic configuration, e.g. a ferromagnet. Hopfield was naturally well aware of how these equations were used to describe magnetic materials.
他注意到许多物理系统的集体属性对模型细节的变化具有鲁棒性,因此利用一个具有 $N$ 二进制节点 $s_i$(0 或 1)的神经网络来解决这个问题。动态变化是异步的,单个节点的阈值更新时间是随机的。节点 $s_i$ 的新值由所有其他节点的加权和决定
$$ h_{i} = \sum_{j\neq i}w_{ij}s_{j}, $$
并且如果 $h_i>0$ 则设置为 $s_i=1$,否则设置为 $s_i=0$(阈值设为零)。耦合 $w_{ij}$ 被假定为对称的,并反映存储记忆中节点之间的成对相关性,这被称为 Hebb 规则。权重的对称性保证了动态的稳定性。平稳状态被识别为记忆,分布在 $N$ 个节点上进行非局部存储。此外,网络被赋予一个能量 $E$,其定义为
$$ E = -\sum_{i<j}w_{ij}s_{i}s_{j} $$
它是在网络动态下单调递减的函数。值得注意的是,20 世纪 80 年代定义的物理世界与人工神经网络之间的联系已经从这两个方程中显而易见。第一个方程可用于表示 Weiss 分子场(以法国物理学家 Pierre Weiss 命名),该场描述了固体中原子磁矩的排列方式,后者通常用于评估磁性配置的能量,例如铁磁体。Hopfield 自然非常清楚这些方程如何用于描述磁性材料。
Metaphorically, the dynamics drive the system with $N$ nodes to the valleys of an $N$-dimensional energy landscape, in which the stationary states are located. The stationary states represent memories learned by the Hebb rule. Initially, the number of memories that could be stored in Hopfield’s dynamical model was limited. Methods to alleviate this problem were developed in later work.
隐喻地说,具有 $N$ 个节点的系统的动态驱动其进入 $N$ 维能量景观的谷底,平稳状态位于其中。平稳状态代表通过 Hebb 规则学习的记忆。最初,Hopfield 动态模型中可以存储的记忆数量是有限的。后来工作中开发了缓解这一问题的方法。
Hopfield used his model as an associative memory or as a method for error correction or pattern completion. A system initialized with an incorrect pattern, perhaps a misspelled word, is attracted to the nearest local energy minimum in his model, whereby a correction occurs. The model gained additional traction when it became clear that basic properties, such as the storage capacity, could be understood analytically, by using methods from spin glass theory.
Hopfield 将他的模型用作联想记忆或错误校正或模式完成的方法。在他的模型中,用不正确的模式(例如拼写错误的单词)初始化的系统会被吸引到最近的局部能量最小值,从而进行纠正。当人们清楚地认识到可以使用自旋玻璃理论的方法来分析理解存储容量等基本属性时,该模型获得了更多的关注。
A legitimate question at the time was whether the properties of this model are an artifact of its crude binary structure. Hopfield answered this question by creating an analog version of the model, with continuous-time dynamics given by the equations of motion for an electronic circuit. His analysis of the analog model demonstrated that the binary nodes could be replaced by analog ones without losing the emergent collective properties of the original model. The stationary states of the analog model corresponded to mean-field solutions of the binary system at an effective adjustable temperature, and approached the stationary states of the binary model at low temperature.
当时一个合理的问题是,这个模型的属性是否是其粗糙二进制结构的产物。Hopfield 通过创建该模型的模拟版本来回答这个问题,其连续时间动态由电子电路的运动方程给出。他对模拟模型的分析表明,二进制节点可以被模拟节点替换,而不会失去原始模型的集体现象。模拟模型的平稳状态对应于二进制系统在有效可调温度下的平均场解,并在低温下接近二进制模型的平稳状态。
The close correspondence between the analog and binary models was subsequently used by Hopfield and David Tank to develop a method for solving difficult discrete optimization problems based on the continuous-time dynamics of the analog model. Here, the optimization problem to be solved, including constraints, is encoded in the interaction parameters (weights) of the network. They chose to use the dynamics of the analog model in order to have a “softer” energy landscape and thereby facilitate the search. The above-mentioned effective temperature of the analog system was gradually decreased, as in global optimization with simulated annealing. Optimization occurs through integration of the equations of motion of an electronic circuit, during which the nodes evolve without instructions from a central unit. This approach constitutes a pioneering example of using a dynamical system to seek solutions to difficult discrete optimization problems. A more recent example is quantum annealing.
模拟和二进制模型之间的密切对应关系随后被 Hopfield 和 David Tank 用来开发一种基于模拟模型的连续时间动态来解决困难的离散优化问题的方法。在这里,要解决的优化问题,包括约束条件,都被编码在网络的相互作用参数(权重)中。他们选择使用模拟模型的动态,以便拥有一个“更柔和”的能量景观,从而促进搜索。上述模拟系统的有效温度逐渐降低,就像使用模拟退火进行全局优化一样。通过集成电子电路的运动方程来进行优化,在此过程中,节点在没有中央单元指令的情况下演化。这种方法构成了使用动态系统来寻找困难离散优化问题解决方案的开创性例子。一个更近的例子是量子退火。
By creating and exploring the above physics-based dynamical models – not only the milestone associative memory model but also those that followed – Hopfield made a foundational contribution to our understanding of the computational abilities of neural networks.
通过创建和探索上述基于物理的动态模型——不仅是里程碑式的联想记忆模型,还有后续的模型——Hopfield 对我们理解神经网络的计算能力做出了奠基性的贡献。
In 1983–1985 Geoffrey Hinton, together with Terrence Sejnowski and other coworkers, developed a stochastic extension of Hopfield’s model from 1982, called the Boltzmann machine. Here, each state $\mathbb{s}=(s_1,\cdots,s_N)$ of the network is assigned a probability given by the Boltzmann distribution
$$ P(\mathbb{s}) \propto e^{-E/T} \quad E = -\sum_{i<j}w_{ij}s_{i}s_{j} - \sum_{i}\theta_{i}s_{i} $$
where $T$ is a fictive temperature and $\theta_{i}$ is a bias, or local field.
1983-1985 年,Geoffrey Hinton 与 Terrence Sejnowski 和其他同事一起,开发了 Hopfield 1982 年模型的随机扩展,称为玻尔兹曼机。在这里,网络的每个状态 $\mathbb{s}=(s_1,\cdots,s_N)$ 都被赋予一个由玻尔兹曼分布给出的概率
$$ P(\mathbb{s}) \propto e^{-E/T} \quad E = -\sum_{i<j}w_{ij}s_{i}s_{j} - \sum_{i}\theta_{i}s_{i} $$
其中 $T$ 是一个虚拟温度,$\theta_{i}$ 是偏置或局部场。
The Boltzmann machine is a generative model. Unlike the Hopfield model, it focuses on statistical distributions of patterns rather than individual patterns. It contains visible nodes that correspond to the patterns to be learned as well as additional hidden nodes, where the latter are included to enable modelling of more general probability distributions.
玻尔兹曼机是一种生成模型。与 Hopfield 模型不同,它关注模式的统计分布而不是单个模式。它包含与要学习的模式对应的可见节点以及额外的隐藏节点,后者被包含在内以实现对更一般概率分布的建模。
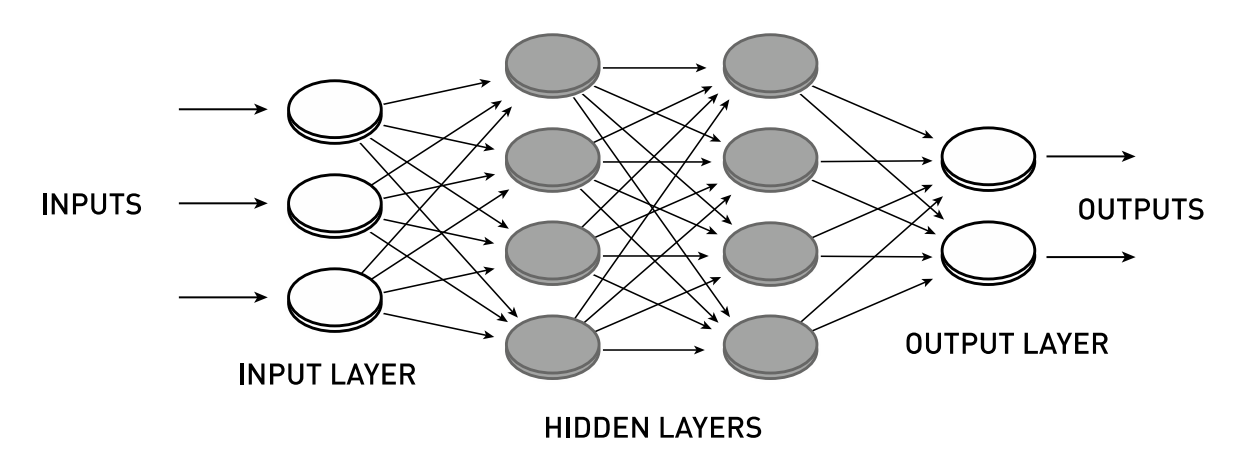
Feedward network with two layers of hidden nodes between the input and output layers.
图 2. 输入层和输出层之间有两层隐藏节点的前馈网络。
The weight and bias parameters of the network, which define the energy $E$, are determined so that the statistical distribution of visible patterns generated by the model deviates minimally from the statistical distribution of a given set of training patterns. Hinton and his colleagues developed a formally elegant gradient-based learning algorithm for the parameter determination; however, each step of the algorithm involves time-consuming equilibrium simulations for two different ensembles.
网络的权重和偏置参数定义了能量 $E$,其确定方式是使模型生成的可见模式的统计分布与给定训练模式集的统计分布之间的偏差最小。Hinton 和他的同事们为参数确定开发了一种形式上优雅的基于梯度的学习算法;然而,该算法的每一步都涉及两个不同集合的耗时平衡模拟。
While theoretically interesting, in practice, the Boltzmann machine was initially of limited use. However, a slimmed-down version of it with fewer weights, called the restricted Boltzmann machine, developed into a versatile tool (see next section).
虽然在理论上很有趣,但在实践中,玻尔兹曼机最初的用途有限。然而,其简化版本,称为受限玻尔兹曼机,具有更少的权重,发展成为一种多功能工具(见下一节)。
Both the Hopfield model and the Boltzmann machine are recurrent neural networks. The 1980s also saw important progress on feedforward networks. A key advance was the demonstration by David Rumelhart, Hinton and Ronald Williams in 1986 of how architectures with one or more hidden layers could be trained for classification using an algorithm known as backpropagation. Here, the objective is to minimize the mean square deviation, $D$, between output from the network and training data, by gradient descent. This requires computing the partial derivatives of $D$ with respect to all weights in the network. Rumelhart, Hinton and Williams reinvented a scheme for this, which had previously been applied to related problems by others. Additionally, and more importantly, they demonstrated that networks with a hidden layer could be trained by this method to perform tasks known to be unsolvable without such a layer. Furthermore, they elucidated the function of hidden nodes.
Hopfield 模型和玻尔兹曼机都是递归神经网络。20 世纪 80 年代还在前馈网络方面取得了重要进展。一个关键的进展是 David Rumelhart、Hinton 和 Ronald Williams 在 1986 年展示了如何使用称为反向传播的算法训练具有一个或多个隐藏层的架构进行分类。在这里,目标是通过梯度下降最小化网络输出与训练数据之间的均方偏差 $D$。这需要计算 $D$ 关于网络中所有权重的偏导数。Rumelhart、Hinton 和 Williams 重新发明了一个方案,之前其他人已经将其应用于相关问题。此外,更重要的是,他们证明了可以通过这种方法训练具有隐藏层的网络来执行已知无法在没有该层的情况下解决的任务。此外,他们阐明了隐藏节点的功能。
Toward deep learning
The methodological breakthroughs in the 1980s were soon followed by successful applications, including pattern recognition in images, languages and clinical data. An important method was multilayered convolutional neural networks (CNN) trained by backpropagation, as advanced by Yann LeCun and Yoshua Bengio. The CNN architecture had its roots in the neocognitron method created by Kunihiko Fukushima, who in turn was inspired by work of David Hubel and Torsten Wiesel, Nobel Prize Laureates in Physiology or Medicine in 1981. The CNN approach developed by LeCun and coworkers became used by several American banks for classifying handwritten digits on checks from the mid-1990s. Another successful example from this period is the long short-term memory method created by Sepp Hochreiter and Jürgen Schmidhuber. This is a recurrent network for processing sequential data, as in speech and language, and can be mapped to a multilayered network by unfolding in time.
20 世纪 80 年代的方法论突破很快就被成功应用,包括图像、语言和临床数据的模式识别。一种重要的方法是由 Yann LeCun 和 Yoshua Bengio 提出的通过反向传播训练的多层卷积神经网络(CNN)。CNN 架构源于福岛邦彦(Kunihiko Fukushima)创建的新认知神经网络(neocognitron)方法,而福岛邦彦的灵感则来自 1981 年诺贝尔生理学或医学奖得主大卫-胡贝尔(David Hubel)和托尔斯滕-维塞尔(Torsten Wiesel)的研究。从 20 世纪 90 年代中期开始,LeCun 及其同事开发的 CNN 方法被几家美国银行用于对支票上的手写数字进行分类。这一时期的另一个成功案例是 Sepp Hochreiter 和 Jürgen Schmidhuber 创造的长短期记忆方法。这是一种用于处理连续数据(如语音和语言)的递归网络,可通过时间展开映射为多层网络。
While certain multilayered architectures led to successful applications in the 1990s, it remained a challenge to train deep multilayered networks with many connections between consecutive layers. To many researchers in the field, training dense multilayered networks seemed out of reach. The situation changed in the 2000s. A leading figure in this breakthrough was Hinton, and an important tool was the restricted Boltzmann machine (RBM).
虽然某些多层架构在 20 世纪 90 年代取得了成功的应用,但训练具有许多连接的深层多层网络仍然是一个挑战。对于该领域的许多研究人员来说,训练密集的多层网络似乎遥不可及。情况在 21 世纪初发生了变化。这一突破的领导人物是 Hinton,而一个重要的工具是受限玻尔兹曼机(RBM)。
An RBM network has weights only between visible and hidden nodes, and no weights connect two nodes of the same type. For RBMs, Hinton created an efficient approximate learning algorithm, called contrastive divergence, which was much faster than that for the full Boltzmann machine. With Simon Osindero and Yee-Whye Teh, he then developed a pretraining procedure for multilayer networks, in which the layers are trained one by one using an RBM. An early application of this approach was an autoencoder network for dimensional reduction. After pre-training, it became possible to perform a global parameter finetuning using the backpropagation algorithm. The pre-training with RBMs picked up structures in data, such as corners in images, without using labelled training data. Having found these structures, labelling those by backpropagation turned out to be a relatively simple task.
RBM 网络只有可见节点和隐藏节点之间的权重,没有权重连接同一类型的两个节点。对于 RBM,Hinton 创建了一种高效的近似学习算法,称为对比散度,其速度远快于完整玻尔兹曼机的学习算法。随后,他与 Simon Osindero 和 Yee-Whye Teh 一起开发了一种多层网络的预训练程序,其中各层使用 RBM 逐一训练。这种方法的一个早期应用是用于降维的自动编码器网络。经过预训练后,可以使用反向传播算法进行全局参数微调。使用 RBM 进行的预训练捕捉到了数据中的结构,例如图像中的角落,而无需使用标记的训练数据。在找到这些结构后,通过反向传播对其进行标记被证明是一个相对简单的任务。
By linking layers pre-trained in this way, Hinton was able to successfully implement examples of deep and dense networks, a milestone toward what is now known as deep learning. Later on, it became possible to replace RBM-based pre-training by other methods to achieve the same performance of deep and dense ANNs.
通过以这种方式链接预训练的层,Hinton 成功地实现了深度和密集网络的示例,这是迈向现在所谓的深度学习的一个里程碑。后来,可以用其他方法替代基于 RBM 的预训练,以实现深度和密集人工神经网络的相同性能。
ANNs as powerful tools in physics and other scientific disciplines
Much of the above discussion is focused on how physics has been a driving force underlying inventions and development of ANNs. Conversely, ANNs are increasingly playing an important role as a powerful tool for modelling and analysis in almost all of physics.
上述讨论的大部分内容都集中在物理学如何成为推动人工神经网络发明和发展的驱动力。相反,人工神经网络作为一种强大的建模和分析工具,在几乎所有物理学领域中发挥着越来越重要的作用。
In some applications, ANNs are employed as a function approximator; i.e. the ANNs are used to provide a “copycat” for the physics model in question. This can significantly reduce the computational resources required, thereby allowing larger systems to be probed at higher resolution. Significant advances have been achieved in this way, e.g. for quantum-mechanical many-body problems. Here, deep learning architectures are trained to reproduce energies of phases of materials, as well as the shape and strength of interatomic forces, with an accuracy comparable to ab initio quantum-mechanical models. With these ANN trained atomic models, considerably faster determination of phase stabilities and the dynamics of new materials can be made. Examples showing the success of these methods involve the prediction of new photovoltaic materials.
在某些应用中,人工神经网络被用作函数逼近器;即,人工神经网络被用来为所讨论的物理模型提供一个“模仿者”。这可以显著减少所需的计算资源,从而允许以更高的分辨率探测更大的系统。通过这种方式取得了显著的进展,例如对于量子力学多体问题。在这里,深度学习架构经过训练以再现材料相的能量,以及原子间力的形状和强度,其精度可与从头算量子力学模型相媲美。通过这些经过人工神经网络训练的原子模型,可以更快地确定新材料的相稳定性和动力学。这些方法成功的例子包括新型光伏材料的预测。
With these models, it is also possible to study phase transitions as well as the thermodynamical properties of water. Similarly, the development of ANN representations has made it possible to reach higher resolutions in explicit physics-based climate models without resorting to additional computing power.
通过这些模型,还可以研究相变以及水的热力学性质。类似地,人工神经网络表示的发展使得在不诉诸额外计算能力的情况下,在显式基于物理的气候模型中达到更高的分辨率成为可能。
During the 1990s, ANNs became a standard data analysis tool within particle physics experiments of ever-increasing complexity. Highly sought-after fundamental particles, such as the Higgs boson, only exist for a fraction of a second after being created in high-energy collisions (e.g. $\sim 10^{-22}$ s for the Higgs boson). Their presence needs to be inferred from tracking information and energy deposits in large electronic detectors. Often the anticipated detector signature is very rare and could be mimicked by more common background processes. To identify particle decays and increase the efficiency of analyses, ANNs were trained to pick out specific patterns in the large volumes of detector data being generated at a high rate.
在 20 世纪 90 年代,人工神经网络成为粒子物理实验中一种标准的数据分析工具,这些实验的复杂性不断增加。备受追捧的基本粒子,如希格斯玻色子,在高能碰撞中产生后只存在一小段时间(例如,希格斯玻色子的寿命约为 $10^{-22}$ 秒)。它们的存在需要通过大型电子探测器中的跟踪信息和能量沉积来推断。通常,预期的探测器信号非常罕见,并且可能被更常见的背景过程所模仿。为了识别粒子衰变并提高分析效率,人工神经网络被训练以从高速生成的大量探测器数据中挑选出特定模式。
ANNs improved the sensitivity of searches for the Higgs boson at the CERN Large ElectronPositron (LEP) collider during the 1990s, and were used in the analysis of data that led to its discovery at the CERN Large Hadron Collider in 2012. ANNs were also used in studies of the top quark at Fermilab.
人工神经网络提高了 20 世纪 90 年代 CERN 大型电子正电子对撞机(LEP)上对希格斯玻色子的搜索灵敏度,并被用于分析导致其在 2012 年 CERN 大型强子对撞机发现的数据。人工神经网络还被用于费米实验室对顶夸克的研究。
In astrophysics and astronomy, ANNs have also become a standard data analysis tool. A recent example is an ANN-driven analysis of data from the IceCube neutrino detector at the South Pole, which resulted in a neutrino image of the Milky Way. Exoplanet transits have been identified by the Kepler Mission using ANNs. The Event Horizon Telescope image of the black hole at the centre of the Milky Way used ANNs for data processing.
在天体物理学和天文学中,人工神经网络也已成为一种标准的数据分析工具。一个最近的例子是对南极冰立方中微子探测器数据的人工神经网络驱动分析,得出了银河系的中微子图像。开普勒任务使用人工神经网络识别了系外行星凌日现象。事件视界望远镜对银河系中心黑洞的成像使用了人工神经网络进行数据处理。
So far, the most spectacular scientific breakthrough using deep learning ANN methods is the AlphaFold tool for prediction of three-dimensional protein structures, given their amino acid sequences. In modelling of industrial physics and chemistry applications, ANNs also play an increasingly important role.
到目前为止,使用深度学习人工神经网络方法取得的最壮观的科学突破是 AlphaFold 工具,它可以根据氨基酸序列预测三维蛋白质结构。在工业物理和化学应用的建模中,人工神经网络也发挥着越来越重要的作用。
ANNs in everyday life
The list of applications used in everyday life that are based on ANNs is long. These networks are behind almost everything we do with computers, such as image recognition, language generation, and more.
基于人工神经网络的日常生活应用清单很长。这些网络支持我们使用计算机进行的几乎所有操作,例如图像识别、语言生成等。
Decision support within health care is also a well-established application for ANNs. For example, a recent prospective randomized study of mammographic screening images showed a clear benefit of using machine learning in improving detection of breast cancer. Another recent example is motion correction for magnetic resonance imaging (MRI) scans.
医疗保健领域的决策支持也是人工智能网络的一个成熟应用。例如,最近一项关于乳房 X 线照相筛查图像的前瞻性随机研究表明,使用机器学习在提高乳腺癌检测率方面有明显的优势。最近的另一个例子是磁共振成像(MRI)扫描的运动校正。
Concluding remarks
The pioneering methods and concepts developed by Hopfield and Hinton have been instrumental in shaping the field of ANNs. In addition, Hinton played a leading role in the efforts to extend the methods to deep and dense ANNs.
Hopfield 和 Hinton 开发的开创性方法和概念在塑造人工神经网络领域方面发挥了重要作用。此外,Hinton 在将这些方法扩展到深度和密集人工神经网络的努力中发挥了领导作用。
With their breakthroughs, that stand on the foundations of physical science, they have showed a completely new way for us to use computers to aid and to guide us to tackle many of the challenges our society face. Simply put, thanks to their work Humanity now has a new item in its toolbox, which we can choose to use for good purposes. Machine learning based on ANNs is currently revolutionizing science, engineering and daily life. The field is already on its way to enable breakthroughs toward building a sustainable society, e.g. by helping to identify new functional materials. How deep learning by ANNs will be used in the future depends on how we humans choose to use these incredibly potent tools, already present in many aspects of our lives.
通过他们的突破,建立在物理科学基础之上,他们为我们展示了一种全新的方式来使用计算机来帮助和指导我们应对社会面临的许多挑战。简单地说,感谢他们的工作,人类现在在其工具箱中有了一件新物品,我们可以选择将其用于良好的目的。基于人工神经网络的机器学习正在彻底改变科学、工程和日常生活。该领域已经在朝着实现突破迈进,以建立一个可持续的社会,例如通过帮助识别新的功能材料。未来深度学习将如何被使用,取决于我们人类如何选择使用这些已经存在于我们生活许多方面的极其强大的工具。
