Polydiversity

$N$:聚合度(degree of polymerization), 即 polymer 的长度

$M_{N}$: 分子质量, 若每个单元的质量为 $M_{MON}$, 则 $M_{N} = NM_{MON}$

$n_{N}$: 数量分数. 即随机抽选一个 polymer, 聚合度为 $N$ 的概率

$w_{N}$: 权重分数,

$$ w_{N} = \frac{n_{N}M_{N}}{\sum_{N}n_{N}M_{N}} = \frac{n_{N}N}{\sum_{N}n_{N}N} $$

K 阶矩(moment):

$$ m_{k} = \sum_{N}n_{N}M_{N}^{k},\quad m_{0} = \sum_{N}n_{N} = 1 $$

数平均质量

$$ M_{n} \equiv \frac{m_{1}}{m_{0}} = \frac{\sum_{N}n_{N}M_{N}}{\sum_{N}n_{N}} = \sum_{M}n_{N}M_{N} $$

加权平均质量

$$ M_{w} \equiv \frac{m_{2}}{m_{1}} = \frac{\sum_{N}n_{N}M_{N}^{2}}{\sum_{N}n_{N}M_{N}} $$

多分散度(Polydiversity Index)

$$ \text{PI} = \frac{M_{w}}{M_{n}} \geq 1 $$

使用 Cauchy-Schwarz 不等式可证明.

$$ \left(\sum_{i=1}^{n}u_{i}^{2}\right)\left(\sum_{i=1}^{n}v_{i}^{2}\right)\geq \left(\sum_{i=1}^{n}u_{i}v_{i}\right) $$

令 $u_{i}=\sqrt{n_{N}}M_{N}$, $v_{i}=\sqrt{n_{N}}$.

Mixing entropy

总数 $A$ 和 $B$ 的物质, 处于态 $|1\rangle, |2\rangle, \cdots$ 的数目各自为 $a_{1},b_{1}$; $a_{2}, b_{2}\cdots$.

混合和分离的状态数依次为

$$ \Omega_{\text{Mix}} = \frac{(A+B)!}{a_{1}!b_{1}!a_{2}!b_{2}!\cdots},\quad \Omega_{\text{Sep}} = \frac{A!}{a_{1}!a_{2}!\cdots}\frac{B!}{b_{1}!b_{2}!\cdots} $$

混合熵

$$ \Delta S_{\text{mix}} = -k_{B}\left( A\ln{\frac{A}{A+B}} + B\ln{\frac{B}{A+B}} \right) $$

令体积分数 $\phi_{A} = \frac{V_{A}}{V_{A}+V_{B}}$, $\phi_{B} = \frac{V_{B}}{V_{A}+V_{B}} = 1 - \phi_{A}$. 若两种物质的基本组成单位体积都是 $v_{0}$, 那么可以约定

$$ n = \frac{V_{A}+V_{B}}{v_{0}} $$

混合熵写作

$$ \Delta S_{\text{mix}} = - k_{B}(n_{A}\ln{\phi_{A}} + n_{B}\ln{\phi_{B}}) $$

每个基本组成单位的混合熵(Entropy of mixing per lattice site)

$$ \Delta \bar{S}_{\text{mix}} = -k_{B}\left[ \frac{\phi_{A}}{N_{A}}\ln{\phi_{A}} + \frac{\phi_{B}}{N_{B}}\ln{\phi_{B}} \right] $$

其中 $N_{A}, N_{B}$ 分别是 $A, B$ 的聚合度(分子长度).

Condensation polynomials

1D random walk polymer

步长 $a$, 步数 $N = n_{l} + n_{r}$, 末端位置 $R = (n_{r} - n_{l})a$.

$$ \begin{aligned} p(R,N) &= \frac{N!}{(\frac{Na+R}{2a})!(\frac{Na-R}{2a})!}\left(\frac{1}{2}\right)^{N}\\ \ln{p} &\approx \ln{\sqrt{\frac{2}{\pi N}}} - \frac{R^{2}}{2Na^{2}}\\ p(R,N) &\approx \sqrt{\frac{2}{\pi N}}\exp{\left(-\frac{R^{2}}{2Na^{2}}\right)} \end{aligned} $$

通过 $\int_{-Na}^{Na}p\mathrm{d}R$ 计算归一化系数为 $2a$. 所以最后的概率密度为

$$ p(R;N) = \sqrt{\frac{1}{2\pi Na^{2}}} \exp{\left(-\frac{R^{2}}{2Na^{2}}\right)} $$

这是一个高斯分布, 均值为 $\bar{R} = 0$, 方差为 $\sigma_{R}^{2} = Na^{2}$.

Freely-jointed chain

Ideal chain. 单元长度 $l$, 段间成角 $\theta$, 则围线长度(contour length) $R_{\text{max}} = nl\cos{\frac{\theta}{2}}$.

Freely jointed chain. 3D random walk.

$$ \langle R^{2} \rangle = \sum_{i,j}\langle \vec{r}_{i}\cdot \vec{r}_{j} \rangle = \sum_{i,j}\langle \cos{\theta_{ij}} \rangle = nl^{2} $$

对于每个单元 $i$, 定义参数 characteristic ratio(特征比)

$$ C_{i}^{\prime} \equiv \sum_{j=1}^{n}\langle \cos{\theta_{ij}}\rangle,\quad C_{n} = \frac{1}{n}\sum_{i=1}^{n}C_{i}^{\prime} $$

这样方均位移为

$$ \langle R^{2}\rangle = l^{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\langle \cos{\theta_{ij}}\rangle = l^{2}\sum_{i=1}^{n}C_{i}^{\prime} = C_{n}nl^{2} $$

长链极限

$$ \langle R^{2}\rangle \approx C_{\infty}nl^{2} $$

定义 Kuhn length $b$, 从而将 Ideal chain 等效为 freely-jointed chain:

$$ Nb = R_{\text{max}},\quad \langle R^{2}\rangle = Nb^{2} = bR_{\text{max}} = C_{\infty}nl^{2} $$

于是反解

$$ N = \frac{R_{\text{max}}^{2}}{C_{\infty}nl^{2}},\quad b = \frac{\langle R^{2}\rangle}{R_{\text{max}}} = \frac{C_{\infty}nl^{2}}{R_{\text{max}}} $$

Freely rotating chain. 固定 $\theta$, 随机 $\phi$.

$$ \langle R^{2}\rangle = nl^{2} + l^{2}\sum_{i=1}^{n}\left( \sum_{k=1}^{i-1}\cos^{k}{\theta} + \sum_{k=1}^{n-i}\cos^{k}{\theta} \right)\simeq nl^{2}\frac{1+\cos{\theta}}{1-\cos{\theta}} $$

persistence segment 长度定义为

$$ s_{p} = -\frac{1}{\ln{\cos{\theta}}} $$

更严谨的定义是

$$ \langle \cos{\theta(s)}\rangle = e^{-s/L_{p}} $$

worm-like chain 是 freely-rotating chain 连接角 $\theta \to 0$ 的极限.

$$ s_{p} = -\frac{1}{\ln{\cos{\theta}}} \simeq \frac{2}{\theta^{2}},\quad l_{p} \equiv s_{p}l = l\frac{2}{\theta^{2}},\quad C_{\infty} = \frac{1+\cos{\theta}}{1-\cos{\theta}} \simeq \frac{2-\theta^{2}/2}{\theta^{2}/2} \simeq \frac{4}{\theta^{2}},\quad b = l\frac{C_{\infty}}{\cos{(\theta/2)}} \simeq l\frac{4}{\theta^{2}} = 2l_{p} $$

Radius of gyration(均方根半径)

$$ \langle R_{g}^{2}\rangle = \frac{1}{N}\sum_{i=1}^{N}\langle (\vec{R}_{i} - \vec{R}_{\text{CM}})^{2}\rangle,\quad \vec{R}_{\text{CM}} = \frac{\sum_{i=1}^{N}M_{i}\vec{R}_{i}}{\sum_{i=1}^{N}M_{i}} $$

另一种计算方式为

$$ R_{g}^{2} = \frac{1}{N^{2}}\sum_{i=1}^{N}\sum_{j=i}^{N}\left(\vec{R}_{i}-\vec{R}_{j}\right)^{2} = \frac{1}{N^{2}}\int_{0}^{N}\mathrm{d}u\int_{u}^{N}\mathrm{d}v\left(\vec{R}(u)-\vec{R}(v)\right)^{2} $$

ideal linear chain:

$$ \langle R_{g}^{2}\rangle = \frac{1}{6}\langle R^{2}\rangle = \frac{1}{6}Nb^{2} = \frac{l_{bp}\xi_{p}}{3} $$

Entropic Force

$$ p(N,x) = \frac{1}{\sqrt{2\pi Na^{2}}}\exp{\left(-\frac{x^{2}}{2Na^{2}}\right)} $$

熵变

$$ \Delta S = k_{B}\ln{\frac{\Omega(N,x)}{\Omega(N,0)}} = k_{B}\ln{\frac{p(N,x)}{p(N,0)}} = -\frac{k_{B}}{2Na^{2}}x^{2} $$

自由能变

$$ \Delta G = \Delta U - T\Delta S = \frac{k_{B}T}{2Na^{2}}x^{2} $$

熵弹性力

$$ f = \frac{\partial G(N,x)}{\partial x} = \frac{k_{B}T}{Na^{2}}x $$

限定该力在 $x\ll Na$ 范围内.

热力学回顾:

$$ H\equiv U+PV,\quad F\equiv U-TS, \quad G\equiv H-TS = U-TS+PV, $$

$$ F = -\frac{\partial G}{\partial L} $$

对于 freely-jointed chain 有 $U,T,P$ 不变, 即

$$ F_{\text{FJC}} = -T\frac{\partial S}{\partial L} $$

Membrane curvature

表面张力: $$\gamma = \frac{F}{L} = \frac{\mathrm{d}W}{\mathrm{d}A}$$

Laplace-Young law: $$\Delta P = \frac{2\gamma}{R}$$

表面方程 $$ \vec{r} = (u,v,h(u,v)) = (x,y,h(x,y)) $$

切向矢量 $$ \vec{r}_{u} = \frac{\partial\vec{r}}{\partial u},\quad \vec{r}_{v} = \frac{\partial\vec{r}}{\partial v} $$

法向矢量 $$ \hat{n} = \frac{\vec{r}_{u}\times \vec{r}_{v}}{|\vec{r}_{u}\times \vec{r}_{v}|} $$

在 Monge gauge 下, 有

$$ \vec{r}_{u} = \vec{r}_{x} = (1,0,h_{x}),\quad \vec{r}_{v} = \vec{r}_{y} = (0,1,h_{y})\\ \mathrm{d}A = \mathrm{d}x\mathrm{d}y\sqrt{1+h^{2}_{x}+h_{y}^{2}} $$

更一般性地,

$$ (\mathrm{d}s)^{2} = (\mathrm{d}\vec{r})^{2} = (\vec{r}_{u}\mathrm{d}u + \vec{r}_{v}\mathrm{d}v)^{2} = E\mathrm{d}u^{2} + 2F\mathrm{d}u\mathrm{d}v + G\mathrm{d}v^{2}\\ E = \left(\frac{\partial\vec{r}}{\partial u}\right)^{2},\quad F = \frac{\partial\vec{r}}{\partial u}\cdot \frac{\partial\vec{r}}{\partial v},\quad G = \left(\frac{\partial\vec{r}}{\partial v}\right)^{2} $$

定义参数 metric(度规) $g$:

$$ g = EG-F^{2} = (\vec{r}_{u}\times \vec{r}_{v})^{2} > 0 $$

那么

$$ \mathrm{d}A = |\vec{r}_{u}\times \vec{r}_{v}|\mathrm{d}u\mathrm{d}v = \sqrt{g}\mathrm{d}u\mathrm{d}v $$

法向矢量

$$ \hat{n} = \frac{\hat{z} - h_{x}\hat{x} - h_{y}\hat{y}}{\sqrt{1+h_{x}^{2}+h_{y}^{2}}} $$

二阶导

$$ \vec{r}^{\prime\prime} = u^{\prime\prime}\vec{r}_{u} + v^{\prime\prime}\vec{r}_{v} + (u^{\prime})^{2}\vec{r}_{uu} + (v^{\prime})^{2}\vec{r}_{vv} + 2(u^{\prime}v^{\prime})\vec{r}_{uv} $$

曲率被定义为 $$ \kappa = \vec{r}^{\prime\prime}\cdot \hat{n} = \frac{L(\mathrm{d}u)^{2}+2M\mathrm{d}u\mathrm{d}v + N(\mathrm{d}v)^{2}}{E(\mathrm{d}u)^{2} + 2F\mathrm{d}u\mathrm{d}v + G(\mathrm{d}v)^{2}}\\ L = -\hat{n}_{u}\cdot \vec{r}_{u},\quad M = -\hat{n}_{u}\cdot \vec{r}_{v},\quad N = -\hat{n}_{v}\cdot \vec{r}_{v} $$

因此曲率也可写作

$$ \kappa = -\frac{\mathrm{d}\vec{r}\cdot\mathrm{d}\hat{n}}{\mathrm{d}\vec{r}\cdot\mathrm{d}\vec{r}} $$

设任意位置矢量 $\hat{a} = l\vec{r}_{u} + m\vec{r}_{v}$. 则该位置的曲率为

$$ \kappa = Ll^{2} + 2Mlm + Nm^{2} $$

因为 $a^{2} = El^{2} + 2Flm + Gm^{2} = 1$, 以此为约束求解 Lagrange 极值:

$$ \widetilde{\kappa} = Ll^{2} + 2Mlm + Nm^{2} - \lambda(El^{2} + 2Flm + Gm^{2}) $$

令 $\partial\widetilde{\kappa}/\partial l = \partial\widetilde{\kappa}/\partial m = 0$ 求得 $l,m$. 于是得到 $\kappa$ 的两个根:

$$ \text{Mean curvature:}\quad H = \frac{EN+GL-2FM}{2(EG-F^{2})}\\ \text{Gaussian curvature:}\quad K = \frac{LN-M^{2}}{EG-F^{2}} $$

若

$$ E = 1+ h_{x}^{2},\quad F = h_{x}h_{y},\quad G = 1+h_{y}^{2}\\ L = \frac{h_{xx}}{\sqrt{1+h_{x}^{2}+h_{y}^{2}}},\quad M = \frac{h_{xy}}{\sqrt{1+h_{x}^{2}+h_{y}^{2}}},\quad N = \frac{h_{yy}}{\sqrt{1+h_{x}^{2}+h_{y}^{2}}} $$

则

$$ H = \frac{(1+h_{x}^{2})h_{yy} + (1+h_{y}^{2})h_{xx} - 2h_{x}h_{y}h_{xy}}{2(1+h_{x}^{2}+h_{y}^{2})^{3/2}},\quad K = \frac{h_{xx}h_{yy} - h_{xy}^{2}}{(1+h_{x}^{2}+h_{y}^{2})^{2}} $$

若 $h_{x}, h_{y} \ll 1$, 则

$$ H\approx \frac{1}{2}(h_{xx} + h_{yy}),\quad K \approx h_{xx}h_{yy} - h_{xy}^{2} $$

表面能

$$ \mathrm{d}E_{\text{surface}} = \left[ \frac{\kappa}{2}\left( \frac{1}{R_{1}} + \frac{1}{R_{2}} - \frac{2}{R_{0}}\right)^{2} + \frac{\kappa_{G}}{R_{1}R_{2}} \right]\mathrm{d}A $$

通过 Hessian 矩阵来处理曲率问题:

2D 曲面

$$ \mathbf{H}(\mathbf{x}) = \begin{pmatrix} \frac{\partial^{2}h}{\partial x^{2}} & \frac{\partial^{2}h}{\partial x\partial y}\\ \frac{\partial^{2}h}{\partial y\partial x} & \frac{\partial^{2}h}{\partial y^{2}} \end{pmatrix} $$

通过求 $\text{det}(\mathbf{H}-\lambda\mathbf{I}) = 0$ 的本征值得到曲率:

$$ \mathbf{H}_{D}(\mathbf{x}) = \begin{pmatrix} \frac{\partial^{2}h}{\partial^{2}a} & 0\\ 0 & \frac{\partial^{2}h}{\partial^{2}b} \end{pmatrix} = \begin{pmatrix} \kappa_{1} & 0\\ 0 & \kappa_{2} \end{pmatrix},\quad \kappa_{1,2} = \frac{1}{R_{1,2}} $$

如何改变 Membrane 最节能?

$$ \begin{aligned} G_{\text{stretch}} = \frac{K_{a}}{2}\frac{\Delta a^{2}}{a_{0}},\quad K_{a}\sim 60kT/\text{nm}^{2}\\ G_{\text{thick}} = \frac{K_{t}}{2}(\frac{\Delta w}{w_{0}})^{2}a_{0},\quad K_{t}\sim 60kT/\text{nm}^{2}\\ G_{\text{bend}} = \frac{K_{b}}{2}\frac{a_{0}}{R^{2}},\quad K_{b}\sim 15kT \end{aligned} $$

Vesicle

$\kappa_{1} = \kappa_{2} = \frac{1}{R}$

$$ G_{\text{bend}} = \frac{K_{b}}{2}\int(2\kappa)^{2}\mathrm{d}a = \frac{K_{b}}{2}\frac{4}{R^{2}}4\pi R^{2} = 8\pi K_{b} $$

Cylinder $\kappa_{1} = 0$, $\kappa_{2} = \frac{1}{R}$

$$ G_{\text{bend}} = \frac{K_{b}}{2}\int\frac{1}{R^{2}}\mathrm{d}a = K_{b}\pi\frac{L}{R} $$

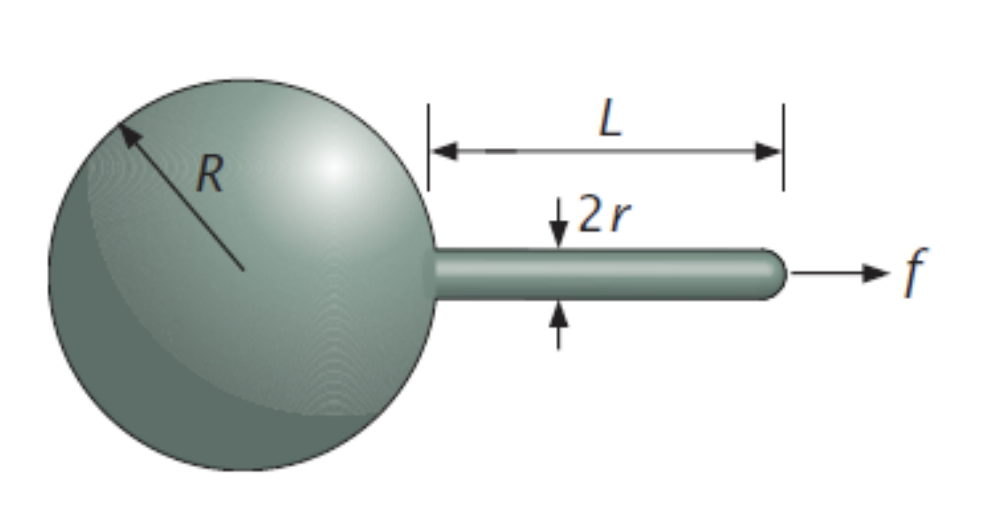
Patch clamp(膜片钳技术)

大囊泡+运输管+小球冠:

$$ \begin{aligned} G_{\text{bend}} &= 8\pi K_{b} + \pi K_{b}\frac{L}{r} + 4\pi K_{b} = 12\pi K_{b} + \pi K_{b}\frac{L}{r}\\ G_{\text{stretch}} &= \frac{K_{a}}{2}\frac{(a-a_{0})^{2}}{a_{0}}\\ G_{pV} &= -\Delta p\left( \frac{4}{3}\pi R^{3} + r^{2}\pi L \right)\\ G_{\text{load}} &= -fL \end{aligned} $$

总能量 $G_{\text{tot}}$ 对各参数偏导均为 0:

$$ \begin{aligned} \frac{\partial G_{\text{tot}}}{\partial R} &= 0\Rightarrow 8\pi\tau R - 4\pi\Delta p R^{2} = 0\\ \frac{\partial G_{\text{tot}}}{\partial r} &= 0\Rightarrow -\pi K_{b}\frac{L}{r^{2}} + 2\pi\tau L - 2\pi\Delta p r L = 0\\ \frac{\partial G_{\text{tot}}}{\partial L} &= 0\Rightarrow \pi K_{b}\frac{1}{r} + 2\pi\tau r - \pi\Delta p r^{2} - f = 0 \end{aligned} $$

其中 $\tau = K_{a}(a-a_{0})/a_{0}$, 解得 $f = 2\pi\sqrt{2K_{b}\tau}$.

Molecular interactions

Covalent bond(共价键), Ionic Bond(离子键), Metallic Bond(金属键), Hydrogen bond(氢键), Dipole‐dipole interactions, Lennard‐Jones potential(范德华力)