GRU
gated recurrent unit.
重置门(reset gate) 更新门(update gate) $\in(0,1)$
广播机制: 对于不同形状的张量, 通过复制扩展使得维度相同.
-
输入 $\mathbf{X}_{t}\in\mathbb{R}^{n\times d}$, 即 batch size(批量维度) 为 $n$, feature dimension(特征维度) 为 $d$
-
隐状态 $\mathbf{H}_{t-1}\in\mathbb{R}^{n\times h}$, 即 batch size 为 $n$, 隐藏单元数 为 $h$
重置门 $\mathbf{R}_{t}\in\mathbb{R}^{n\times h}$ 和更新门 $\mathbf{Z}_{t}\in\mathbb{R}^{n\times h}$ 的计算公式: $$ \begin{aligned} \overset{n\times h}{\mathbf{R}_{t}} &= \sigma(\overset{n\times d}{\mathbf{X}_{t}}\cdot\overset{d\times h}{\mathbf{W}_{xr}} + \overset{n\times h}{\mathbf{H}_{t-1}}\cdot\overset{h\times h}{\mathbf{W}_{hr}} + \overset{1\times h}{\mathbf{b}_{r}}),\\ \overset{n\times h}{\mathbf{Z}_{t}} &= \sigma(\overset{n\times d}{\mathbf{X}_{t}}\cdot\overset{d\times h}{\mathbf{W}_{xz}} + \overset{n\times h}{\mathbf{H}_{t-1}}\cdot\overset{h\times h}{\mathbf{W}_{hz}} + \overset{1\times h}{\mathbf{b}_{z}})\\ \sigma(x) &= \frac{1}{1+e^{-x}}, \quad \text{sigmoid function} \end{aligned} $$
其中, $\mathbf{b}$ 会通过广播扩展为 $n\times h$ 的矩阵.
常规的隐状态更新: $$ \mathbf{H}_{t} = \phi(\mathbf{X}_{t}\cdot\mathbf{W}_{xh} + \mathbf{H}_{t-1}\cdot \mathbf{W}_{hh} + \mathbf{b}_{h}) $$
候选隐状态 $\widetilde{\mathbf{H}}_{t}\in\mathbb{R}^{n\times h}$ 计算:
$$ \overset{n\times h}{\widetilde{\mathbf{H}}_{t}} = \tanh{(\mathbf{X}_{t}\mathbf{W}_{xh} + (\mathbf{R}_{t}\odot \mathbf{H}_{t-1})\cdot \mathbf{W}_{hh} + \mathbf{b}_{h})} $$
Hadamard 积 $\odot$:
$$ \begin{bmatrix} a_{11} & {\color{red}{a_{12}}} & a_{13}\\ {\color{blue}{a_{21}}} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix}\odot\begin{bmatrix} b_{11} & {\color{red}{b_{12}}} & b_{13}\\ {\color{blue}{b_{21}}} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} & {\color{red}{a_{12}b_{12}}} & a_{13}b_{13}\\ {\color{blue}{a_{21}b_{21}}} & a_{22}b_{22} & a_{23}b_{23}\\ a_{31}b_{31} & a_{32}b_{32} & a_{33}b_{33} \end{bmatrix} $$
隐状态 $\mathbf{H}_{t}$ 计算:
$$ \overset{n\times h}{\mathbf{H}_{t}} = \overset{n\times h}{\mathbf{Z}_{t}} \odot \overset{n\times h}{\mathbf{H}_{t-1}} + (1-\overset{n\times h}{\mathbf{Z}_{t}})\odot \overset{n\times h}{\widetilde{\mathbf{H}}_{t}} $$
注意力机制
- 查询(Query): 自主性提示
- 键(Key): 非自主性提示
- 值(Value): 感官输入
对于数据集 $\{(x_{i},y_{i})\}$, 如何学习其规律 $f$ 以预测任意输入 $x$ 的输出 $\hat{y} = f(x)$?
Nadaraya-Watson 核:
$$ f(x) = \sum_{i=1}^{n}\frac{K(x-x_{i})}{\sum_{j=1}^{n}K(x-x_{j})}y_{i} $$
或写作 注意力汇聚 形式:
$$ f(x) = \sum_{i=1}^{n}\alpha(x,x_{i})y_{i} $$
$\alpha(x,x_{i})$ 被称作 注意力权重, 那么 $f(x)$ 是对所有 $y_{i}$ 的加权平均.
比如考虑 Gaussian 核 $\begin{aligned}K(u) = \frac{1}{\sqrt{2\pi}}\exp{(-\frac{u^2}{2})}\end{aligned}$, 学习的 $f$:
$$ \begin{aligned} f(x) &= \sum_{i=1}^{n}\alpha(x,x_{i})y_{i}\\ &= \sum_{i=1}^{n}\frac{\exp{[-(x-x_{i})^{2}/2}]}{\sum_{j=1}^{n}\exp{[-(x-x_{j})^{2}/2]}}y_{i}\\ &= \sum_{i=1}\text{softmax}\left(-\frac{1}{2}(x-x_{i})^{2}\right)y_{i} \end{aligned} $$
也可引入参数 $w$ 调整核的宽度:
$$ \begin{aligned} f(x) &= \sum_{i=1}^{n}\alpha(x,x_{i})y_{i}\\ &= \sum_{i=1}^{n}\frac{\exp{[-w^{2}(x-x_{i})^{2}/2}]}{\sum_{j=1}^{n}\exp{[-w^{2}(x-x_{j})^{2}/2]}}y_{i}\\ &= \sum_{i=1}\text{softmax}\left(-\frac{1}{2}w^{2}(x-x_{i})^{2}\right)y_{i} \end{aligned} $$
Gaussian 核指数部分被称作 attention scoring function.
假设有 $m$ 个 key-value 对 $\{(\mathbf{k}_{i},\mathbf{v}_{i})\}$, 其中 $\mathbf{k}_{i}\in\mathbb{R}^{k}$, $\mathbf{v}_{i}\in\mathbb{R}^{v}$.
给定查询 $\mathbf{q}\in\mathbb{R}^{q}$, 则注意力汇聚函数为
$$ \begin{aligned} f(\mathbf{q},(\mathbf{k}_{1},\mathbf{v}_{1}),\cdots,(\mathbf{k}_{m},\mathbf{v}_{m})) &= \sum_{i=1}^{m}\alpha(\mathbf{q},\mathbf{k_{i}})\mathbf{v}_{i} \in \mathbb{R}^{v}\\ \alpha(\mathbf{q},\mathbf{k}_{i}) = \text{softmax}[a(\mathbf{q},\mathbf{k}_{i})] &= \frac{\exp{[a(\mathbf{q},\mathbf{k}_{i})]}}{\sum_{j=1}^{m}\exp{[a(\mathbf{q},\mathbf{k}_{j})]}}\in\mathbb{R} \end{aligned} $$
$a$ 即为注意力评分函数.
Masked softmax operation(掩码 softmax 操作): 仅将有意义的键值对纳入到计算中.
比如在语句处理中, 指定最长序列长度, 从而在计算 softmax 时过滤超过范围的部分(超出指定长度的位置均设为 $0$).
加性注意力: Query 和 Key 长度不同($q\neq k$). 注意力评分函数定义为
$$ a(\mathbf{q},\mathbf{k}) = \overset{1\times h}{\mathbf{w}_{v}^{\top}}\tanh{(\overset{h\times q}{\mathbf{W}_{q}}\cdot\overset{q\times 1}{\mathbf{q}} + \overset{h\times k}{\mathbf{W}_{k}}\cdot\overset{k\times 1}{\mathbf{k}})} $$
缩放点积注意力: Query 和 Key 长度都为 $d$.
若 Q 和 K 的元素均为独立随机变量, 且都是零均值, 单位方差. 那么 Q 与 K 的点积将是零均值, 方差为 $d$. 为了方差仍未 1, 将点积归一化, 则形成 scaled dot-product attention:
$$ a(\mathbf{q},\mathbf{k}) = \frac{\mathbf{q}^{\top}\mathbf{k}}{\sqrt{d}} $$
在批量处理时, 则学习到的注意力汇聚函数为
$$ \text{softmax}\left(\frac{\overset{n\times d}{\mathbf{Q}}\cdot\overset{d\times m}{\mathbf{K}^{\top}}}{\sqrt{d}}\right)\overset{m\times v}{\mathbf{V}} $$
自注意力: Value = Key. 其注意力汇聚函数会输出等长序列:
$$ \mathbf{y}_{i} = f(\mathbf{x}_{i},(\mathbf{x}_{1},\mathbf{x}_{1}),\cdots, (\mathbf{x}_{n},\mathbf{x}_{n}))\in \mathbb{R}^{d} $$
位置编码: 自注意力是并行计算的, 因此对顺序是无知的.
$$ a_{m,n} = \frac{\exp{\left(\frac{q_{m}^{\top}k_{n}}{\sqrt{d}}\right)}}{\sum_{j=1}^{N}\exp{\left(\frac{q_{m}^{\top}k_{j}}{\sqrt{d}}\right)}} $$
如果任意地打乱 $x$ 顺序, 对应的 $q$ 和 $k$ 也会对应地打乱, 但是 $q^{\top}k$ 是仍然不变的, 这就是对 token 顺序和间距不敏感的表现.
因此, 我们希望对词语引入有关位置的信息, 即 $q_{m}\rightarrow f(q,m)$, $k_{n}\rightarrow f(k,n)$, 于是注意力评分函数变为
$$ a_{m,n} = \frac{\exp{\left(\frac{f(q,m)^{\top}f(k,n)}{\sqrt{d}}\right)}}{\sum_{j=1}^{N}\exp{\left(\frac{f(q,m)^{\top}f(k,j)}{\sqrt{d}}\right)}} $$
- 基于三角函数的 固定位置编码
若有一个输入为 $\mathbf{X}\in \mathbb{R}^{n\times d}$, 其含有 $n$ 个词元, 每个词元被嵌入表达为一个 $d$ 维的向量. 那么定义位置嵌入矩阵 $\mathbf{P}\in\mathbb{R}^{n\times d}$:
$$ \begin{aligned} p_{i,2j} &= \sin{\left(\frac{i}{10000^{2j/d}}\right)}\\ p_{i,2j+1} &= \cos{\left(\frac{i}{10000^{2j/d}}\right)} \end{aligned} $$
然后将输出 $\mathbf{X} + \mathbf{P}$ 作为后续计算的输入.
- 旋转位置编码 RoPE(Rotary Position Embedding): 将一个向量旋转一个和位置有关的角度
RoPE 希望将 $q_{m}^{\top}k_{n}$ 携带上相对位置 $(m-n)$ 的信息, 即寻找函数 $f$ 使得
$$ f(q,m)\cdot f(k,n) = g(q,k,m-n) $$
而旋转矩阵满足这个性质.
假设 $q\in\mathbb{R}^{2}$, 则
$$ f(q,m) = R_{m}q = \begin{bmatrix} \cos{m\theta} & -\sin{m\theta}\\ \sin{m\theta} & \cos{m\theta} \end{bmatrix}\begin{bmatrix} q_{1}\\ q_{2} \end{bmatrix} $$
注意到
$$ \begin{aligned} q_{m}^{\top}k_{n} &= f(q,m)^{\top}f(k,n) = (R_{m}q)^{\top}\cdot (R_{n}k) = q^{T}R_{m}^{\top}R_{n}k\\ &= q^{\top}\begin{bmatrix} \cos{m\theta} & -\sin{m\theta}\\ \sin{m\theta} & \cos{m\theta} \end{bmatrix}^{\top}\begin{bmatrix} \cos{n\theta} & -\sin{n\theta}\\ \sin{n\theta} & \cos{n\theta} \end{bmatrix}k\\ &= q^{\top}\begin{bmatrix} \cos{(n-m)\theta} & -\sin{(n-m)\theta}\\ \sin{(n-m)\theta} & \cos{(n-m)\theta} \end{bmatrix}k\\ &= q^{\top}R_{n-m}k \end{aligned} $$
若要推广至更高维度, 可将 $d$ 维向量元素两两一组, 从而获得高维向量的旋转:
$$ \begin{aligned} \begin{bmatrix} \cos{m\theta} & -\sin{m\theta} & 0 & 0 & \cdots & 0 & 0\\ \sin{m\theta} & \cos{m\theta} & 0 & 0 & \cdots & 0 & 0\\ 0 & 0 & \cos{m\theta} & -\sin{m\theta} & \cdots & 0 & 0\\ 0 & 0 & \sin{m\theta} & \cos{m\theta} & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & 0 & 0 & \cdots & \cos{m\theta} & -\sin{m\theta}\\ 0 & 0 & 0 & 0 & \cdots & \sin{m\theta} & \cos{m\theta} \end{bmatrix}\begin{bmatrix} q_{1}\\ q_{2}\\ q_{3}\\ q_{4}\\ \vdots\\ q_{d-1}\\ q_{d} \end{bmatrix} \end{aligned} $$
若将 $\theta$ 替换为与维度有关的 $\theta_{j} = 10000^{-2j/d}$, 则可得到最终的 RoPE 位置编码方式.
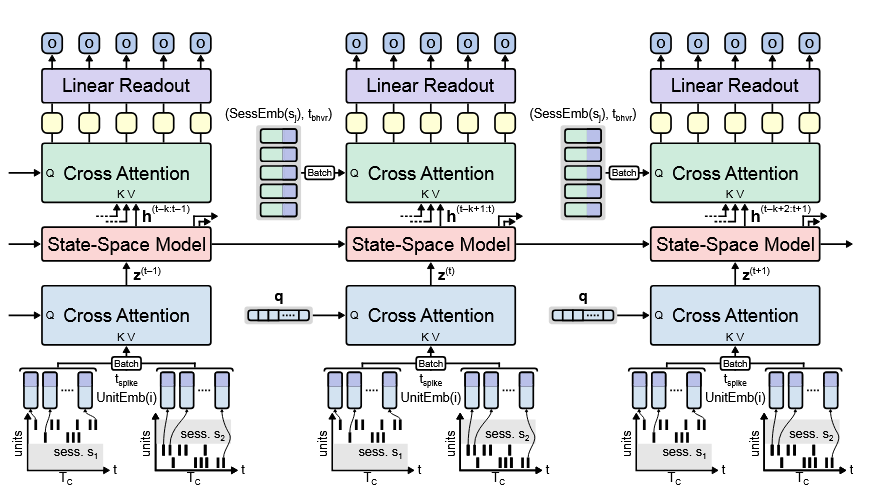
数据读取
如何将 50ms 的 spikes 数据转为一个 $D$ 维的 latent 向量?
$$ \mathbf{x}_{n} = \text{RoPE}[\text{UnitEmb}(u_{n}),\Delta t_{n}] $$
其中 $u_{n}$ 为第 $n$ 个通道(channel)的编号, $\Delta t_{n}$ 为该通道内 spikes 的相对时间(相对于各 bin 起始时间).
# Model.py
self.emb = nn.Embedding(
num_embeddings=meta_data["num_channel"],
embedding_dim=config.embed_dim
)
解码 & 输出
最近 $k$ 个隐状态(State-Space Model 或者 Gated Recurrent Unit) 作为元素, 形成张量
$$ \mathbf{H} = [\mathbf{h}_{t-k+1}, \mathbf{h}_{t-k+2}, \cdots, \mathbf{h}_{t}]\in\mathbb{R}^{k\times h} $$
取一个时间块(bin) 内的 $T_{c}$ 个点.
Key & Value:
$$ \mathbf{K} = \mathbf{H}\cdot\mathbf{W}_{k},\quad \mathbf{V} = \mathbf{H}\cdot\mathbf{W}_{v} $$