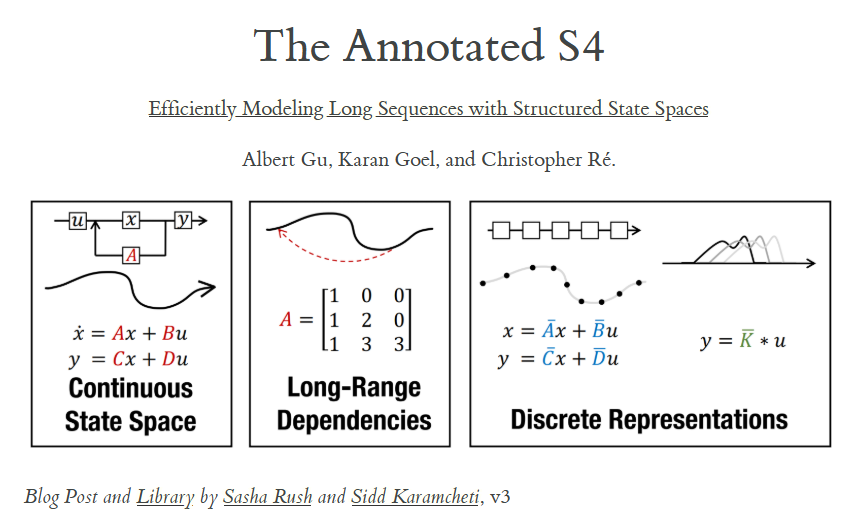
状态空间模型 Space State Model
$u(t)$: 一维输入信号
$x(t)$: $N$ 维隐状态
$y(t)$: 一维输出信号
$$ \begin{aligned} x^{\prime}(t) &= \mathbf{A}x(t) + \mathbf{B}u(t)\\ y(t) &= \mathbf{C}x(t) + \mathbf{D}u(t) \end{aligned} $$
注意这里的 $x^{\prime}$ 是对时间求导数, 亦即 $\begin{aligned}\frac{\mathrm{d}x(t)}{\mathrm{d}t}\end{aligned}$. 需要将其和后面离散化时的下标区分开来.
$\mathbf{A}, \mathbf{B}, \mathbf{C}, \mathbf{D}$ 通过 gradient descent 学习. 下文中略去 $\mathbf{D}$ 项(这种与因变量无关而输入-输出呈现直达关系, 被称作 skip connection).
离散时间的状态空间模型(Discrete-time SSM)
将对时间连续的输入信号 $u(t)$ 离散/采样为 $(u_{0},u_{1},\cdots)$. 若通过 $\Delta$ (步长 step size) 表达采样的分辨率, 那么 $u_{k} = u(k\Delta)$.
现在将原本的微分方程转化为差分方程:
$$ \begin{aligned} x_{k} &= \mathbf{\bar{A}}x_{k-1} + \mathbf{\bar{B}}u_{k}\\ y_{k} &= \mathbf{\bar{C}}x_{k} \end{aligned} $$
这里 $x_{k}, u_{k}, y_{k}$ 都是离散变量.
我们通过 双线性变换(Bilinear Transform) 来完成这一步.
朴素直觉的差分方法是
$$ \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t} &= \mathbf{A}x+\mathbf{B}u\\ \Rightarrow \frac{x_{k+1}-x_{k}}{\Delta} &= \mathbf{A}x_{k} + \mathbf{B}u_{k}\\ \Rightarrow x_{k+1} &= (\mathbf{I} + \Delta \mathbf{A})x_{k} + \Delta \mathbf{B}u_{k} \end{aligned} $$
这种思想即欧拉法.
Tustin 法是这样处理的:
$$ \begin{aligned} \frac{x_{k+1}-x_{k}}{\Delta} &\approx \mathbf{A}\frac{x_{k+1}+x_{k}}{2} + \mathbf{B}u_{k}\\ \Rightarrow (\mathbf{I}-\frac{\Delta}{2}\mathbf{A})x_{k+1} &= (\mathbf{I} + \frac{\Delta}{2}\mathbf{A})x_{k} + \Delta \mathbf{B}u_{k}\\ \Rightarrow x_{k+1} &= {\color{red}{(\mathbf{I}-\frac{\Delta}{2}\mathbf{A})^{-1}(\mathbf{I}+\frac{\Delta}{2}\mathbf{A})}}x_{k} + {\color{blue}{(\mathbf{I}-\frac{\Delta}{2}\mathbf{A})^{-1}\Delta \mathbf{B}}}u_{k}\\ &= {\color{red}{\mathbf{\bar{A}}}}x_{k} + {\color{blue}{\mathbf{\bar{B}}}}u_{k}\\ \end{aligned} $$
而对于方程组的第二个等式, 由于没有任何差分处理, 所以 $\mathbf{\bar{C}} = \mathbf{C}$. 于是得到离散模型的矩阵:
$$ \begin{aligned} \mathbf{\bar{A}} &= (\mathbf{I}-\frac{\Delta}{2}\mathbf{A})^{-1}(\mathbf{I}+\frac{\Delta}{2}\mathbf{A})\\ \mathbf{\bar{B}} &= (\mathbf{I}-\frac{\Delta}{2}\mathbf{A})^{-1}\Delta \mathbf{B}\\ \mathbf{\bar{C}} &= \mathbf{C} \end{aligned} $$
这和 RNN 的数学形式 $h_{k} = f(W_{h}h_{k-1} + W_{x}u_{k})$ 非常相似[取 $f(x) = x$]. 将这样的一次计算称为 step.
在 Python 中, slice 对数据类型的维数变化:
原始数据类型 slice 后的数据类型 $(L,)$ ()(即标量) $(L,1)$ $(1,)$ $(L,N)$ $(N,)$ $(L,B,N)$ $(B,N)$
力学算例
对于一维振子:
$$ my^{\prime\prime}(t) = u(t) - by^{\prime}(t) - ky(t) $$
$y(t)$: 位置, $y^{\prime}(t)$: 速度, $y^{\prime\prime}(t)$: 加速度
$u(t)$: 外力, $m$: 质量, $b$: 阻尼系数, $k$: 弹性系数
可以将其重写为 SSM 形式, 其中
$$ \mathbf{A} = \begin{bmatrix} 0 & 1\\ -\frac{k}{m} & -\frac{b}{m} \end{bmatrix},\quad \mathbf{B} = \begin{bmatrix} 0\\ \frac{1}{m} \end{bmatrix},\quad \mathbf{C} = \begin{bmatrix} 1 & 0 \end{bmatrix} $$
定义状态矢量
$$ \vec{x}(t) = \begin{bmatrix} x_{1}(t)\\ x_{2}(t) \end{bmatrix} = \begin{bmatrix} y(t)\\ y^{\prime}(t) \end{bmatrix} $$
在这里其实已经和传统物理学中使用的相空间概念 $\{\vec{p},\vec{q}\}$ 一致了. 我们可对原方程中的各变量进行替换:
$$ y^{\prime\prime}(t) = x_{2}^{\prime}(t), \quad y^{\prime}(t) = x_{2}(t),\quad y(t) = x_{1}(t) $$
整理振动方程, 与固有求导关系组成 SSM 方程组:
$$ \begin{aligned} \begin{cases} x_{1}^{\prime}(t) &= x_{2}(t)\\ m x_{2}^{\prime}(t) &= u(t) - b x_{2}(t) - k x_{1}(t) \end{cases}\\ \Rightarrow \begin{cases} x_{1}^{\prime}(t) &= 0\cdot x_{1}(t) + 1 \cdot x_{2}(t)\\ x_{2}^{\prime}(t) &= -\frac{k}{m} x_{1}(t) - \frac{b}{m} x_{2}(t) + \frac{1}{m} u(t) \end{cases}\\ \Rightarrow \begin{bmatrix} x_{1}^{\prime}(t)\\ x_{2}^{\prime}(t) \end{bmatrix} = {\color{red}{\begin{bmatrix} 0 & 1\\ -\frac{k}{m} & -\frac{b}{m} \end{bmatrix}}} \begin{bmatrix} x_{1}(t)\\ x_{2}(t) \end{bmatrix} + {\color{blue}{\begin{bmatrix} 0\\ \frac{1}{m} \end{bmatrix}}} u(t) \end{aligned}\\ \Rightarrow \vec{x}^{\prime}(t) = {\color{red}{\mathbf{A}}}\vec{x}(t) + {\color{blue}{\mathbf{B}}}u(t) $$
因为关注的结果是位置, 因此有关系
$$ y(t) = x_{1}(t) = 1\cdot x_{1}(t) + 0 \cdot x_{2}(t) $$
我们可以通过求矢量内积的方式得到输出:
$$ y(t) = {\color{green}{\begin{bmatrix} 1 & 0 \end{bmatrix}}} \begin{bmatrix} x_{1}(t)\\ x_{2}(t) \end{bmatrix} = {\color{green}{\mathbf{C}}}\vec{x}(t) $$
由此推得 $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$ 矩阵形式.
最朴素的定义函数的方法是
def f(x):
return x + 1
Python 允许将函数作为值定义给另一个变量
g = f # g(3) == 4
Python 可通过 lambda 定义匿名函数.
lambda x: x + 1
等价于
def _(x):
return x + 1
也可通过 lambda 定义变量. (函数很短, 不用大费力气专门 def)
h = lambda x : x + 1 # h(3) == 4
partial 是用来固定函数某些传入参数.
from functools import partial
def add(x, y):
return x + y
add10 = partial(add, 10) # 固定 x = 10
add10(5) # == add(10, 5) == 15
通过 lambda 实现等效功能:
add10 = lambda y: add(10, y)
训练 SSM: 卷积表述(Convolutinal Representation)
前面的 scan 形式的伪代码大概可以写作
for k = 0 to L-1:
x_k = A @ x_{k-1} + B @ u_k
y_k = C @ x_k
这种循环迭代是以串行的方式完成的. 而卷积计算方式具有并行的特性.
linear time-invariant(LTI): 线性时间守恒.
LTI SSM 与连续卷积有关, 因此 recurrent SSM 也可写作离散卷积形式.
recall: 差分形式 SSM 方程 $$ \begin{aligned} x_{k} &= \mathbf{\bar{A}}x_{k-1} + \mathbf{\bar{B}}u_{k}\\ y_{k} &= \mathbf{\bar{C}}x_{k} \end{aligned} $$
设 $x_{-1} = 0$. 计算前 3 步:
$$ \begin{aligned} \begin{cases} x_{0} &= \mathbf{\bar{A}}x_{-1} + \mathbf{\bar{B}}u_{0} = \mathbf{\bar{B}}u_{0}\\ x_{1} &= \mathbf{\bar{A}}x_{0} + \mathbf{\bar{B}}u_{1} = \mathbf{\bar{A}}\mathbf{\bar{B}}u_{0} + \mathbf{\bar{B}}u_{1}\\ x_{2} &= \mathbf{\bar{A}}x_{1} + \mathbf{\bar{B}}u_{2} = \mathbf{\bar{A}}^{2}\mathbf{\bar{B}}u_{0} + \mathbf{\bar{A}}\mathbf{\bar{B}}u_{1} + \mathbf{\bar{B}}u_{2}\\ \end{cases},\quad \begin{cases} y_{0} &= \mathbf{\bar{C}}x_{0} = \mathbf{\bar{C}}\mathbf{\bar{B}}u_{0}\\ y_{1} &= \mathbf{\bar{C}}x_{1} = \mathbf{\bar{C}}\mathbf{\bar{A}}\mathbf{\bar{B}}u_{0} + \mathbf{\bar{C}}\mathbf{\bar{B}}u_{1}\\ y_{2} &= \mathbf{\bar{C}}x_{2} = \mathbf{\bar{C}}\mathbf{\bar{A}}^{2}\mathbf{\bar{B}}u_{0} + \mathbf{\bar{C}}\mathbf{\bar{A}}\mathbf{\bar{B}}u_{1} + \mathbf{\bar{C}}\mathbf{\bar{B}}u_{2}\\ \end{cases} \end{aligned} $$
观察递推形式, 可知
$$ \begin{aligned} x_{k} &= \sum_{j=0}^{k}\mathbf{\bar{A}}^{k-j}\mathbf{\bar{B}}u_{j}\\ y_{k} &= \mathbf{\bar{C}}x_{k} = \sum_{j=0}^{k}\mathbf{\bar{C}}\mathbf{\bar{A}}^{k-j}\mathbf{\bar{B}}u_{j} = \mathbf{\bar{C}}\mathbf{\bar{A}}^{k}\mathbf{\bar{B}}u_{0} + \mathbf{\bar{C}}\mathbf{\bar{A}}^{k-1}\mathbf{\bar{B}}u_{1} + \cdots + \mathbf{\bar{C}}\mathbf{\bar{A}}^{0}\mathbf{\bar{B}}u_{k} \end{aligned} $$
也可写作卷积形式:
$$ \begin{aligned} y &= \mathbf{\bar{K}} * u\\ \mathbf{\bar{K}} &= (\mathbf{\bar{C}\bar{B}}, \mathbf{\bar{C}\bar{A}\bar{B}}, \mathbf{\bar{C}\bar{A}}^{2}\mathbf{\bar{B}}, \cdots, \mathbf{\bar{C}\bar{A}}^{L-1}\mathbf{\bar{B}})\\ u &= (u_{0}, u_{1}, \cdots, u_{L-1}) \end{aligned} $$
对于离散序列 $K = \{K_{0}, K_{1}, \cdots, K_{L-1}\}$ 和 $u = \{u_{0}, u_{1}, \cdots, u_{L-1}\}$, 它们的离散卷积定义为
$$ y = K * u = K_{0} u_{L-1} + K_{1} u_{L-2} + \cdots + K_{L-1} u_{0} = \sum_{j=0}^{L-1} K_{j} u_{L-1-j} $$
其中 $\mathbf{\bar{K}}$ 被称为 SSM 卷积核(convolution kernel) 或滤波器(filter). 它与序列等长, 因此是很大的.
利用卷积定理还能再将计算进一步加快. 序列越长, FFT 加速效果越好 [$\mathcal{O}(L\log{L})$].
$$ \mathcal{F}(K*u) = \mathcal{F}(K) \odot \mathcal{F}(u) $$
FFT 假设序列具有周期性. 而 SSM 是非周期(对于有限长度序列, 超出序列长度外都被填充为 0)的.
- 线性卷积
一般性的线性卷积 $y = x * h$ 被定义为
$$ y_{n} = \sum_{k=-\infty}^{\infty}x_{k}h_{n-k} $$
而对于有限序列, 定义输入序列 $\{x_{n}\}$, 长度 $N$; 滤波器/卷积核 $\{h_{n}\}$, 长度 $M$. 那么线性卷积为
$$ y_{n} = \sum_{k=0}^{N-1}x_{k}h_{n-k},\quad h_{n-k} = \begin{cases} h_{n-k}, & n-k \in [0, M-1]\\ 0, & \text{otherwise} \end{cases} $$
$h$ 相当于只取和 $x$ 有重叠部分的值进行计算.
卷积定义 当然也可以写作这种形式:
$$ y_{n} = \sum_{\underset{i+j=n}{i,j}} x_{i}h_{j} $$
那么, 我们可以得到
$$ \begin{aligned} y_{0} &= x_{0}h_{0}\\ y_{1} &= x_{0}h_{1} + x_{1}h_{0}\\ y_{2} &= x_{0}h_{2} + x_{1}h_{1} + x_{2}h_{0}\\ &\vdots \\ y_{N+M-3} &= x_{N-2}h_{M-1} + x_{N-1}h_{M-2}\\ y_{N+M-2} &= x_{N-1}h_{M-1} \end{aligned} $$
这就是为什么输出序列 $\{y_{n}\}$ 会有 $N+M-2-0+1 = N+M-1$ 个元素.
[Example] 离散卷积计算
$x = [1, 2, 3], h = [4, 5 ,6]$.
$$ \begin{aligned} y_{0} &= x_{0}h_{0} = 1\cdot 4 = 4\\ y_{1} &= x_{0}h_{1} + x_{1}h_{0} = 1\cdot 5 + 2\cdot 4 = 13\\ y_{2} &= x_{0}h_{2} + x_{1}h_{1} + x_{2}h_{0} = 1\cdot 6 + 2\cdot 5 + 3\cdot 4 = 28\\ y_{3} &= x_{1}h_{2} + x_{2}h_{1} = 2\cdot 6 + 3\cdot 5 = 27\\ y_{4} &= x_{2}h_{2} = 3\cdot 6 = 18 \end{aligned} $$
这个过程也可以理解为求多项式乘积的系数:
$$ \begin{aligned} h(x) &= (x_{0} + x_{1}x + x_{2}x^{2} + \cdots)\cdot(h_{0} + h_{1}x + h_{2}x^{2} + \cdots)\\ &= x^{0}(x_{0}h_{0}) \\ &+ x^{1}(x_{0}h_{1} + x_{1}h_{0}) \\ &+ x^{2}(x_{0}h_{2} + x_{1}h_{1} + x_{2}h_{0}) + \cdots \end{aligned} $$
将 $x$ 替换为复数 $e^{-\frac{2\pi i}{N}}$, 可得到 DFT 形式的卷积计算. 因为这些系数具有周期性, 因此计算更快.
- FFT 卷积
对于 $a = [a_{0}, a_{1}, a_{2}, \cdots, a_{n-1}]$ 和 $b = [b_{0}, b_{1}, b_{2}, \cdots, b_{m-1}]$, 分别代表多项式
$$ \begin{aligned} f(x) &= a_{0} + a_{1}x + a_{2}x^{2} + \cdots + a_{n-1}x^{n-1}\\ g(x) &= b_{0} + b_{1}x + b_{2}x^{2} + \cdots + b_{m-1}x^{m-1} \end{aligned} $$
现在通过 FFT 计算 $\{a\}$ 和 $\{b\}$ 的离散傅里叶变换:
$$ \begin{aligned} \hat{a} &= [\hat{a}_{0}, \hat{a}_{1}, \hat{a}_{2}, \cdots, \hat{a}_{m+n-1}]\\ \hat{b} &= [\hat{b}_{0}, \hat{b}_{1}, \hat{b}_{2}, \cdots, \hat{b}_{m+n-1}]\\ \text{DFT: }\hat{a}_{k} &= \sum_{n=0}^{L-1} a_{n}w_{k}^{n}, \quad w_{k} = e^{-\mathrm{i} 2\pi\frac{k}{L}}\\ \end{aligned} $$
也就是说, DFT 相当于多项式 $f(x)$ 与 $g(x)$ 在 $\{w_{k}\}$ 单位圆上采样.
然后对 $\hat{a}$ 和 $\hat{b}$ 进行点乘:
$$ \hat{a}\cdot\hat{b} = [\hat{a}_{0}\hat{b}_{0}, \hat{a}_{1}\hat{b}_{1}, \hat{a}_{2}\hat{b}_{2}, \cdots, \hat{a}_{m+n-1}\hat{b}_{m+n-1}] $$
最后对结果进行逆 FFT, 即可得到 $a$ 和 $b$ 的卷积结果:
$$ a * b = \text{IFFT}\left(\hat{a}\cdot\hat{b}\right) = \begin{bmatrix} a_{0}b_{0}\\ a_{0}b_{1} + a_{1}b_{0}\\ a_{0}b_{2} + a_{1}b_{1} + a_{2}b_{0}\\ \vdots\\ a_{n-1}b_{m-1} \end{bmatrix} $$
[Example] 还是以 $a = [1, 2, 3], b = [4, 5 ,6]$ 为例, 过一遍计算的流程. 由于序列长度 $L = m+n-1 = 5$, 因此需要对 $a$ 和 $b$ 进行 zero-padding:
$$ a = [1, 2, 3, 0, 0],\quad b = [4, 5, 6, 0, 0] $$
其多项式为
$$ f(x) = 1 + 2x + 3x^{2}\\ g(x) = 4 + 5x + 6x^{2} $$
取 $w_{k} = e^{-\frac{2\pi i}{L}k} = e^{-\frac{2\pi i}{5}k}$, 依次计算:
$$ \begin{aligned} w_{0} = e^{0} = 1:\quad \hat{a}_{0} &= f(w_{0}) = 1 + 2 + 3 = 6\\ \hat{b}_{0} &= g(w_{0}) = 4 + 5 + 6 = 15\\ \hat{c}_{0} &= \hat{a}_{0}\hat{b}_{0} = 6 \cdot 15 = 90\\ w_{1} = e^{-\frac{2\pi i}{5}}:\quad \hat{a}_{1} &= f(w_{1}) = 1 + 2e^{-\frac{2\pi i}{5}} + 3e^{-\frac> {4\pi i}{5}}\\ \hat{b}_{1} &= g(w_{1}) = 4 + 5e^{-\frac{2\pi i}{5}} + 6e^{-\frac{4\pi i}{5}}\\ \hat{c}_{1} &= \hat{a}_{1}\hat{b}_{1}\\ &\vdots \end{aligned} $$
将 $f(w_{k})$ 和 $g(w_{k})$ 点乘组成序列 $\{h(w_{k})\} = \{f(w_{k})g(w_{k})\}$.
既然
$$ h(x) = f(x)g(x) = c_{0} + c_{1}x + c_{2}x^{2} + c_{3}x^{3} + c_{4}x^{4} $$
那么 $\{h(w_{k}) = f(w_{k})g(w_{k})\}$ 实际构成了具有 5 个方程的方程组, 以求解所需系数 $\{c_{i}\}$.
$$ h(w_{k}) = \hat{c}_{k} = \sum_{n=0}^{4}c_{n}w_{k}^{n} $$
其逆变换为
$$ c_{n} = \frac{1}{5}\sum_{k=0}^{4}\hat{c}_{k}w_{k}^{-n} = \frac{1}{5}\sum_{k=0}^{4}h(w_{k})w_{k}^{-n} $$
因果系统被定义为: 在时间 $k$ 内, 输出 $y_{k}$ 不能依赖未来输入. 即
$$ y_{k} = \sum_{i=0}^{k} K_{i}u_{k-i},\quad i\leq k $$
比如已知 $u = \{u_{0}, u_{1}, u_{2},\cdots, u_{L-1}\}$ 的情况下, 代表 $k\geq L$ 时, $y_{k}$ 的计算将会用到未定义的 $u_{k-i}$.
SSM Neural Network
$\mathbf{A}$: 通过 HiPPO 进行固定, 而不是通过学习来调整.
$\mathbf{B}$, $\mathbf{C}$, $\Delta$, $D$: 通过学习获得.
- 层归一化(Layer Normalization).
设模型内某层, 某时刻流动的数据(token)为 $\vec{x}\in\mathbb{R}^{d}$. LayerNorm 被定义为
$$ \mathrm{LN}(\vec{x}) = \vec{\gamma} \odot \frac{\vec{x}-{\color{red}{\mu}}}{{\color{red}{\sigma}}} + \vec{\beta} $$
$\gamma$, $\beta$ 是模型的可训练参数.
recall: $\odot$ 的定义
$$ \begin{bmatrix}a_{1}\\ a_{2}\\\cdots\\a_{d}\end{bmatrix} \odot \begin{bmatrix}b_{1}\\ b_{2}\\\cdots\\b_{d}\end{bmatrix} = \begin{bmatrix}a_{1}b_{1}\\ a_{2}b_{2}\\\cdots\\a_{d}b_{d}\end{bmatrix} $$
$$ \mu = \frac{1}{d}\sum_{i=1}^{d}x_{i}, \quad \sigma = \sqrt{\frac{1}{d}\sum_{i=1}^{d}(x_{i}-\mu)^{2} + \epsilon} $$
$\epsilon$ 是一个很小的数, 避免 $\vec{x}-\mu$ 除以 0.
prenorm 和 postnorm 的数学形式比较:
$$ \begin{aligned} \text{prenorm:}\quad x_{l+1} &= x_{l} + F[\mathrm{LN}(x_{l})]\\ \text{postnorm:}\quad x_{l+1} &= \mathrm{LN}(x_{l} + F[x_{l}]) \end{aligned} $$
- 残差连接(Residual Connection).
一般的网络层可以约化为
$$ \vec{y} = F(\vec{x}), \quad\vec{x}\in\mathbb{R}^{d} $$
而残差的思想是
$$ \vec{y} = \vec{x} + F(\vec{x}) $$
$F(\vec{x}) = 0$ 即 $\vec{y}$ 是 $\vec{x}$ 的恒等映射.
离散动力学系统的数学形式和 ResNet 的非常相似:
$$ \vec{x}_{k+1} = \vec{x}_{k} + \Delta t\cdot f(\vec{x}_{k}) $$
残差 $\vec{x}_{k}$ 和变化量 $\Delta \vec{x}$ 必定是同维度的.
- Dense Layer.
序列层的输出 $\vec{h} = seq(\vec{x})$ 和残差维数是不同的. 这就需要
$$ \Delta \vec{x} = \mathbf{W}\cdot \vec{h} + \vec{b} $$
- GLU 门控
$$ \Delta\vec{x} = (\mathbf{W}_{1}\cdot\vec{h}+\vec{b}_{1})\odot \sigma(\mathbf{W}_{2}\cdot\vec{h} + \vec{b}_{2}) $$
在该网页的教学示例代码中, 是通过 $\mathbf{W}_{1} = \mathbf{W}_{2}$, $\vec{b}_{1} = \vec{b}_{2}$ 做到的.